Bài 7 trang 69 SGK Toán 9 tập 1

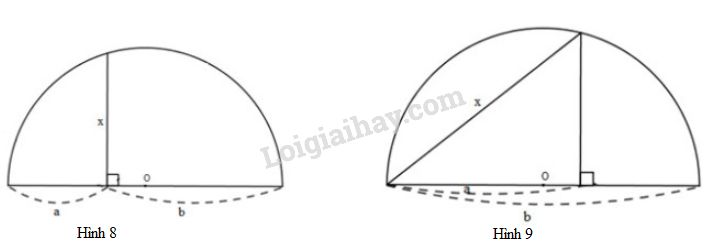
Đề bài

Người ta đưa ra hai cách vẽ đoạn trung bình nhân \(x\) của hai đoạn thẳng \(a,\ b\) (tức là \({x^2} = ab\) ) như trong hai hình sau:

Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Lời giải chi tiết

Cách 1: Đặt tên các đoạn thẳng như hình bên. 

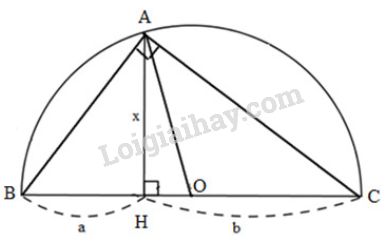
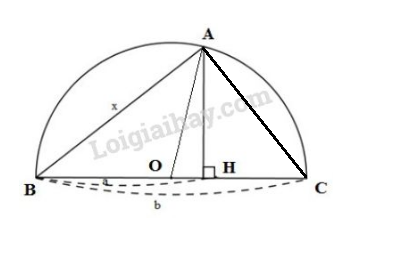
Xét \(\Delta{ABC}\) có: 

      \(OA = OB = OC = \dfrac{BC}{2}\) (cùng bằng bán kính đường tròn (O))

Mà \(AO\) là trung tuyến ứng với cạnh \(BC\) của \(\Delta{ABC}\).

Suy ra \(\Delta{ABC}\) vuông tại \(A\) ( tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì là tam giác vuông)

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

       \(AH^2=BH.CH \Leftrightarrow x^2=a.b\)

                                       \(\Leftrightarrow x=\sqrt {ab}\)

Vậy \(x\) là trung bình nhân của \(a\) và \(b\).

Cách vẽ: Bước \(1\): Đặt \(BH=a,\ CH=b\). Xác định trung điểm \(O\) của đoạn \(AB\). 

             Bước \(2\): Vẽ nửa đường tròn tâm \(O\) bán kính \(OB\). 

             Bước \(3\): Kẻ thẳng đi qua \(H\) và vuông góc với \(BC\). Đường thẳng này cắt nửa đường tròn tại \(A\). 

             Bước \(4\): Nối \(A\) và \(H\) ta được \(AH=x\) là đoạn trung bình nhân của hai đoạn thẳng \(a,\ b\).

Cách 2: Vẽ và đặt tên như hình bên dưới

Xét \(\Delta{ABC}\) có:

                \(OA = OB = OC = \dfrac{BC}{2} \) (cùng bằng bán kính đường tròn (O))

Mà \(AO\) là trung tuyến ứng với cạnh \(BC\) của \(\Delta{ABC}\).

Suy ra \(\Delta{ABC}\) vuông tại \(A\) (tam giác có đường trung tuyến ứng với cạnh huyền bẳng nửa cạnh đó thì là tam giác vuông)

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\).  Áp dụng hệ thức \(b^2=b'.a\), ta có:

                 \(AB^2 = BC.BH \Leftrightarrow x^2=a.b\)

                                                \(\Leftrightarrow x=\sqrt{ab}\) 

Vậy \(x\) là trung bình nhân của \(a\) và \(b\).

Cách vẽ: Bước \(1\): Đặt \(BH=a,\ CH=b\). Xác định trung điểm \(O\) của đoạn \(BC\).

             Bước \(2\): Vẽ nửa đường tròn tâm \(O\) bán kính \(OB\). 

             Bước \(3\): Kẻ đường thẳng đi qua điểm \(H\) và vuông góc với \(BC\). Đường thẳng này cắt nửa đường tròn tại \(A\). 

             Bước \(4\): Nối \(B\) và \(A\) ta được \(AB=x\) là đoạn trung bình nhân của hai đoạn thẳng \(a,\ b\). 

Loigiaihay.com