Bài 6 trang 169 Tài liệu dạy – học Toán 7 tập 1Giải bài tập Cho góc xOy có số đo Quảng cáo
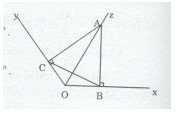
Đề bài Cho góc xOy có số đo \({120^0}\) , lấy điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox \((B \in 0x)\) , kẻ AC vuông góc Oy \((C \in Oy)\). Tam giác ABC là tam giác gì ? Vì sao ? Lời giải chi tiết Gọi Oz là tia phân giác của góc xOy \(\Rightarrow \widehat {AOB} = \widehat {COA} = {1 \over 2}\widehat {xOy} = {60^0}\) Tam giác OAB có: \(\widehat {OBA} = {90^0}\) vì \(AB \bot 0x\) Nên \(\widehat {OAB} + \widehat {AOB} = {90^0} \Rightarrow \widehat {OAB} = {90^0} - \widehat {AOB} = {30^0}.\) Tam giác OAC có: \(\widehat {AOC} = {90^0}\) vì \(AC \bot Oy\) Nên \(\widehat {OAC} + \widehat {COA} = {90^0} \Rightarrow \widehat {OAC} = {90^0} - \widehat {COA} = {30^0}\) Xét tam giác OAB và OAC ta có: \(\widehat {OAB} = \widehat {OAC}( = {30^0})\) OA là cạnh chung. \(\widehat {AOB} = \widehat {COA}( = {60^0})\) Do đó: \(\Delta OAB = \Delta OAC(g.c.g) \Rightarrow AB = AC \Rightarrow \Delta ABC\) cân tại A. Mặt khác \(\widehat {BAC} = \widehat {OAB} + \widehat {OAC} = {30^0} + {30^0} = {60^0}\) Do đó: tam giác ABC là tam giác đều. Loigiaihay.com
|




















Danh sách bình luận