Bài 40 trang 27 SGK Toán 9 tập 2Giải các hệ phương trình sau và minh họa hình học kết quả tìm được: Quảng cáo
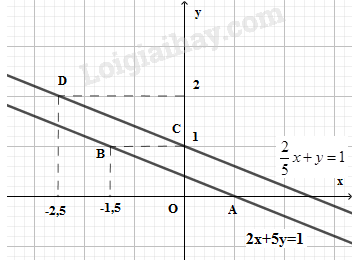
Video hướng dẫn giải Giải các hệ phương trình sau và minh họa hình học kết quả tìm được: LG a \(\left\{ \matrix{2{\rm{x}} + 5y = 2 \hfill \cr {\displaystyle{2 \over 5}}x + y = 1 \hfill \cr} \right.\) Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số để tìm nghiệm Minh họa hình học: Tức là ta biểu thị 2 đường thẳng trên cùng hệ trục tọa độ. Lời giải chi tiết: Giải hệ phương trình: \(\left\{ \matrix{ Cộng vế với vế của hai phương trình trong hệ trên, ta được: \(2x + 5y +(-2x-5y)= 2-5 \) \( \Leftrightarrow 0 = - 3\) (vô lý) Vậy hệ đã cho vô nghiệm. Minh họa hình học kết quả tìm được:
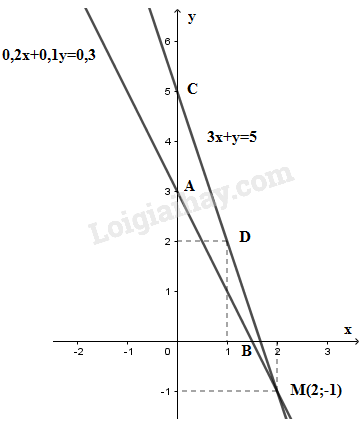
- Vẽ đồ thị hàm số \(2x + 5y = 2\). Cho \(y = 0 ⇒ x = 1\). Ta xác định được điểm \(A(1; 0)\) Cho \(y = 1 ⇒ x = -1,5\). Ta xác định được điểm \(B(-1,5; 1)\). Đồ thị hàm số \(2x + 5y = 2\) là đường thẳng đi qua hai điểm A và B -Vẽ đồ thị hàm số \({\displaystyle{2 \over 5}}x + y = 1 \Leftrightarrow 2{\rm{x}} + 5y = 5\) Cho \(x = 0 ⇒ y = 1\). Ta xác định được điểm \(C(0; 1)\) Cho \(y = 2 ⇒ x = -2,5\). Ta xác định được điểm \(D(-2,5; 2)\) Đồ thị hàm số \({\displaystyle{2 \over 5}}x + y = 1\) là đường thẳng đi qua hai điểm C và D. Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm. LG b \(\left\{ \matrix{0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right.\) Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số để tìm nghiệm Minh họa hình học: Tức là ta biểu thị 2 đường thẳng trên cùng hệ trục tọa độ. Lời giải chi tiết: Giải hệ phương trình: \(\left\{ \matrix{ Cộng vế với vế của hai phương trình trên, ta được \(-2x-y+3x+y=-3+5\) \( \Leftrightarrow x = 2\) Thế \(x = 2\) vào phương trình (2), ta được: \(6 + y = 5 ⇔ y = -1\) Vậy nghiệm của hệ phương trình là \((x;y)=(2;-1)\) Minh họa hình học:
- Đồ thị hàm số \(0,2x + 0,1y = 0,3\) là một đường thẳng đi qua hai điểm: \(A( 0; 3)\) và \(B(1,5; 0)\) - Đồ thị hàm số \(3x + y = 5\) là một đường thẳng đi qua hai điểm \(C( 0; 5)\) và \(D( 1; 2)\) - Đồ thị hai hàm số trên cắt nhau tại điểm: \(M( 2; -1)\). Vậy \((2; -1)\) là một nghiệm của hệ phương trình. LG c \(\left\{ \matrix{{\displaystyle{3 \over 2}}x - y = {\displaystyle{1 \over 2}} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\) Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số để tìm nghiệm Minh họa hình học: Tức là ta biểu thị 2 đường thẳng trên cùng hệ trục tọa độ. Lời giải chi tiết: Giải hệ phương trình: \(\left\{ \matrix{ \( \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 1\\ - 3x + 2y + 3x - 2y = - 1 + 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}2y = 3x - 1\\0 = 0\left( {luôn \, đúng} \right)\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{3}{2}x - \dfrac{1}{2}\\x \in \mathbb{R}\end{array} \right.\) Vậy hệ phương trình đã cho có vô số nghiệm. Nghiệm tổng quát là \(\left( {x;{\displaystyle{3 \over 2}}x - {\displaystyle{1 \over 2}}} \right)\) với \(x ∈ R\) Minh họa hình học
- Đồ thị hàm số \(\dfrac{3}{2}x - y = \dfrac{1}{2}\) và đồ thị hàm số \(3x - 2y = 1\) cùng là một đường thẳng đi qua hai điểm \(A(0; - {\displaystyle{1 \over 2}})\) và \(B(1;1)\) nên hai đường thẳng này trùng nhau. Vậy hệ phương trình có vô số nghiệm. Loigiaihay.com
|














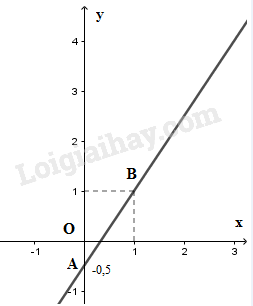






Danh sách bình luận