Bài 4 trang 134 SGK Toán 9 tập 2

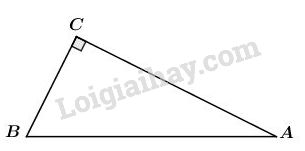
Đề bài

Nếu tam giác vuông $ABC$ vuông tại $C$ và có $\displaystyle \sin {\rm{A}} = {2 \over 3}$ thì $tan B$ bằng:

(A) $\displaystyle {3 \over 5}$            (B) $\displaystyle {{\sqrt 5 } \over 3}$            (C) $\displaystyle{2 \over {\sqrt 5 }}$         (D) $\displaystyle {{\sqrt 5 } \over 2}$                

Hãy chọn câu trả lời đúng. 

Lời giải chi tiết

 

Trong tam giác vuông $ABC$ $\left( {\widehat C = {{90}^0}} \right)$, ta có:

$\displaystyle \sin {\rm{A}} = {{BC} \over {AB}} = {2 \over 3} \Rightarrow AB = {3 \over 2}BC$ 

Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có: 

$\eqalign{ & AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{\left( {{3 \over 2}BC} \right)}^2} - B{C^2}} \cr & AC = \sqrt {{5 \over 4}B{C^2}} = {{BC\sqrt 5 } \over 2} \cr}$

Ta có:  $\displaystyle \tan B = {{AC} \over {BC}} = {{\displaystyle BC{{\sqrt 5 } \over \displaystyle 2}} \over {BC}} = {{\sqrt 5 } \over 2}$  

Chọn đáp án D.

Loigiaihay.com