Bài 35: Ôn tập chung (tiết 1) trang 130 vở bài tập Toán 5 - Kết nối tri thứcViết hỗn số thích hợp vào chỗ chấm (theo mẫu) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
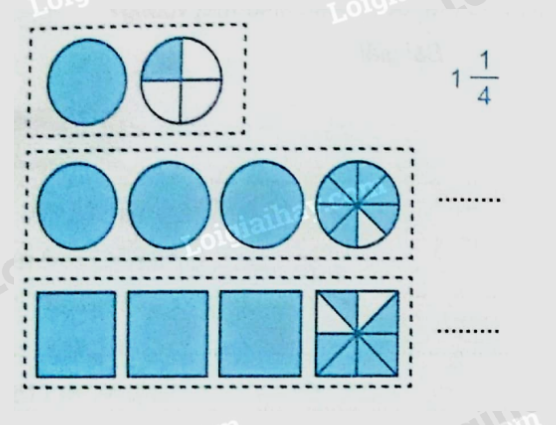
Bài 1 Giải Bài 1 trang 130 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống a) Viết hỗn số thích hợp vào chỗ chấm (theo mẫu)
b) Chuyển các hỗn số: 4$\frac{2}{{5}}$; 7$\frac{3}{{10}}$; 5$\frac{19}{{100}}$ thành phân số. c) Chuyển các phân số: $\frac{123}{{50}}$; $\frac{116}{{200}}$; $\frac{37}{{125}}$ thành số thập phân.
Phương pháp giải: a) Quan sát hình và viết hỗn số thích hợp theo mẫu. b) Tách hỗn số thành phần nguyên cộng với phần phân số rồi tính. c) Chuyển các phân số đã cho thành phân số thập phân, sau đó viết phân số thập phân thành hỗn số rồi viết thành số thập phân thích hợp. Lời giải chi tiết: a)  b)
b) c)  Bài 2 Giải Bài 2 trang 130 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống Tính a) $\frac{6}{{11}}$+$\frac{3}{{5}}$ b) $\frac{3}{{7}}$+$\frac{4}{{9}}$ c) $\frac{8}{{9}}$-$\frac{4}{{5}}$ d) $\frac{15}{{9}}$-$\frac{3}{{5}}$ Phương pháp giải: Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi cộng (hoặc trừ) hai phân số đó. Lời giải chi tiết: a) $\frac{6}{{11}}$+$\frac{3}{{5}}$=$\frac{30}{{55}}$+$\frac{33}{{55}}$=$\frac{63}{{55}}$ b) $\frac{3}{{7}}$+$\frac{4}{{9}}$=$\frac{27}{{63}}$+$\frac{28}{{63}}$=$\frac{55}{{63}}$ c) $\frac{8}{{9}}$ -$\frac{4}{{5}}$= $\frac{40}{{45}}$-$\frac{36}{{45}}$=$\frac{4}{{45}}$ d) $\frac{15}{{9}}$-$\frac{3}{{5}}$=$\frac{75}{{45}}$-$\frac{27}{{45}}$=$\frac{16}{{15}}$ Bài 3 Giải Bài 3 trang 131 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống Tính bằng cách thuận tiện a) $\frac{5}{{17}} + \frac{{18}}{{11}} + \frac{{12}}{{17}}$ b) $\frac{4}{7} \times \frac{{14}}{{19}} + \frac{4}{7} \times \frac{5}{{19}}$ Phương pháp giải: a) Áp dụng tính chất giao hoán, kết hợp của phép cộng để nhóm hai phân số có cùng mẫu số với nhau. b) Áp dụng công thức a × b + a × c = a × (b + c) Lời giải chi tiết: Bài 4 Giải Bài 4 trang 131 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống Trong một đợt thu gom giấy vụn, lớp 5A đã thu gom được 54 kg giấy vụn, lớp 5B đã thu gom được số giấy vụn bằng $\frac{7}{{9}}$ số giấy vụn của lớp 5A, lớp 5C thug om được nhiều hơn lớp 5B là 10 kg. Biết 1 kg giấy vụn làm được 12 cuốn vở tái chế. Hỏi số giấy vụn của cả ba lớp làm được bao nhiêu cuốn vở tái chế? Phương pháp giải: Tính số giấy vụn lớp 5B thu gom được = số giấy vụn lớp 5A × $\frac{7}{{9}}$ Tính số giấy vụn lớp 5C thu gom được = số giấy vụn lớp 5B + 10 kg Tính tổng số giấy vụn của cả ba lớp. Tính số cuốn vở tái chế làm được = Tổng số ki-lô-gam giấy vụn × 12 Lời giải chi tiết: Bài giải Lớp 5B thu gom được số giấy vụn là: 54 × $\frac{7}{{9}}$ = 42 (kg) Lớp 5C thu gom được số giấy vụn là: 42 + 10 = 52 (kg) Cả ba lớp thu gom được số giấy vụn là: 54 + 42 + 52 = 148 (kg) Số giấy vụn của cả ba lớp làm được số cuốn vở tái chế là: 148 × 12 = 1 776 (cuốn) Đáp số: 1 776 cuốn vở
|














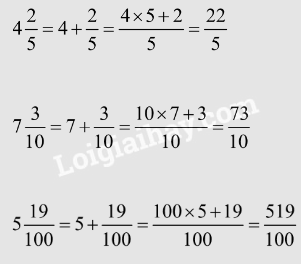
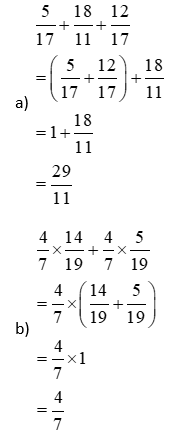






Danh sách bình luận