Bài 34 trang 119 SGK Toán 9 tập 1

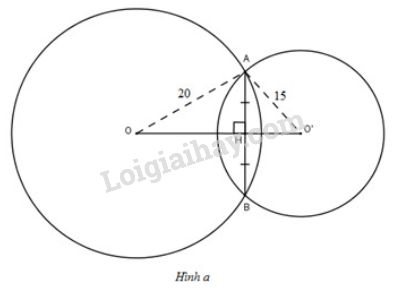
Đề bài

Cho hai đường tròn \((O;\ 20cm)\) và \((O'; 15cm)\) cắt nhau tại \(A\) và \(B\). Tính đoạn nối tâm \(OO'\), biết rằng \(AB=24cm.\) (Xét hai trường hợp: \(O\) và \(O'\) nằm khác phía đối với \(AB;\ O\) và \(O'\) nằm cùng phía đối với \(AB\)). 

Lời giải chi tiết

* TH1:  \(O\) và \(O'\) nằm khác phía đối với \(AB\) (h.a) 

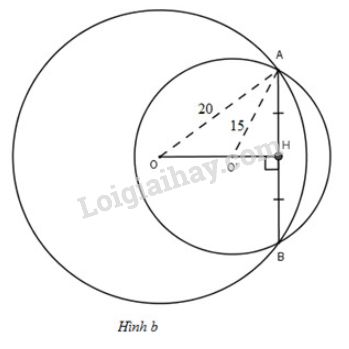
Vẽ dây cung \(AB\) cắt \(OO'\) tại \(H\). Theo định lí - trang 119 về tính chất đường nối tâm, ta có:  \(AB\perp OO'\) và \(HA=HB=\dfrac{24}{2}=12cm\).

Xét tam giác \(AOH\) vuông tại \(H\), áp dụng định lí Pytago, ta có:

\(OA^2=OH^2+AH^2 \)

\(\Rightarrow OH^2=OA^2-AH^2=20^{2}-12^{2}=256\)

\(\Leftrightarrow OH=\sqrt{256}=16cm.\)

Xét tam giác \(AO'H\) vuông tại \(H\), áp dụng định lí Pytago, ta có:

\(AO'^2=AH^2+HO'^2\)

\(\Rightarrow HO'^2=AO'^2 - AH^2=15^2-12^2=81\)

\(\Leftrightarrow HO'=\sqrt {81}=9(cm)\).

Khi đó  \(OO'=OH+HO'=16+9=25(cm).\)

*TH2: \(O\) và \(O'\) nằm cùng phía đối với \(AB\) (h.b)

Tương tự TH1 ta vẫn có \(OH=16cm;O'H=9cm\)

Khi đó \(OO'=OH-O'H=16-9=7(cm).\)