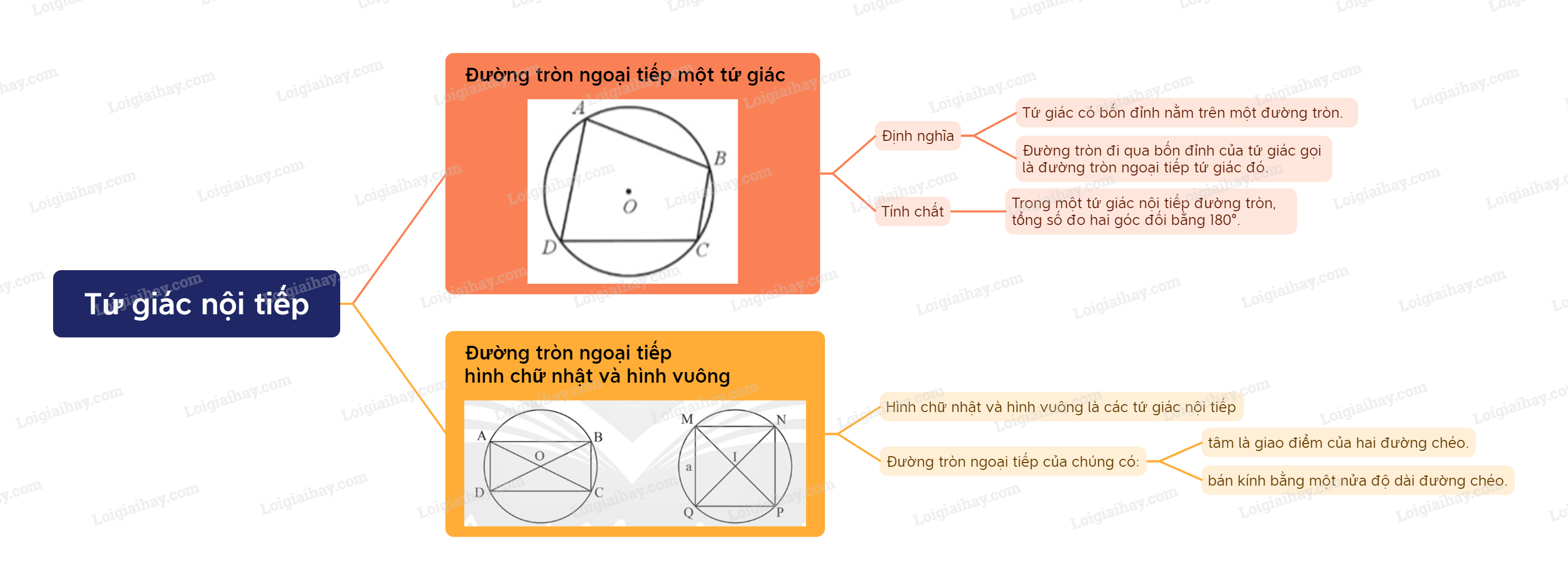
Lý thuyết Tứ giác nội tiếp Toán 9 Chân trời sáng tạo1. Đường tròn ngoại tiếp của một tứ giác Định nghĩa đường tròn ngoại tiếp tứ giác - Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp). - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó. Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Quảng cáo
1. Đường tròn ngoại tiếp của một tứ giác Định nghĩa đường tròn ngoại tiếp tứ giác
Ví dụ:
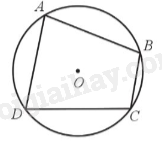
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD. Tính chất
Ví dụ:
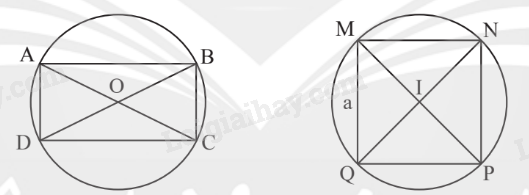
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \). 2. Đường tròn ngoại tiếp hình chữ nhật và hình vuông
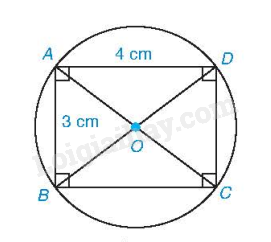
Ví dụ:
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta có: \(B{D^2} = A{B^2} + A{D^2} = {3^2} + {4^2} = 25\) nên \(BD = 5cm\). Do đó, ta có \(R = \frac{{BD}}{2} = 2,5cm\). Đường tròn (O;2,5) là đường tròn ngoại tiếp hình chữ nhật ABCD.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
