Lý thuyết Tích phân Toán 12 Cùng khám phá

1. Khái niệm tích phân

Một số bài toán dẫn đến khái niệm tích phân

a) Quãng đường đi được của một vật

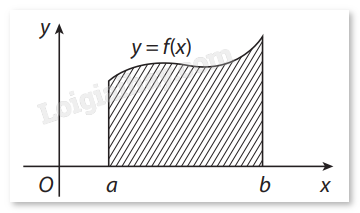
Xét một vật chuyển động thẳng với vận tốc v = v(t) (0 < t < T) và không đổi chiều chuyển động. Gọi F(t) là một nguyên hàm bất kỳ của v(t) trên khoảng (0;T) thì quãng đường vật đi được từ thời điểm t = a đến thời điểm t = b là L = F(b) − F(a) với 0 < a < b < T.

b) Diện tích hình thang cong

Cho hàm số  f(x) liên tục trên đoạn [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x = a, x = b được gọi là hình thang cong.

Trong trường hợp tổng quát, cho hàm số y = f(x) liên tục, không âm trên đoạn [a;b], người ta chứng minh được rằng diện tích hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và các đường thẳng x = a, x = b bằng F(b) − F(a), với F(x) là một nguyên hàm của f(x) trên đoạn [a;b].

Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f(x) = {x^2} + 1\) và các đường thẳng x = -1, x = 2.

Định nghĩa tích phân

Ta còn dùng ký hiệu F(x) để chỉ hiệu số F(b) − F(a).

Vậy \(\int\limits_a^b {f(x)dx}  = F(x)\left| {\begin{array}{*{20}{c}}b\\a\end{array}} \right. = F(b) - F(a)\).

Ta gọi \(\int\limits_a^b {} \) là dấu tích phân, a là cận dưới, b là cận trên, \(f\left( x \right)dx\) là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

Ghi chú:

- Quy ước: \(\int\limits_a^0 {f(x)dx}  = 0\), nếu b > a thì \(\int\limits_b^a {f(x)dx}  =  - \int\limits_a^b {f(x)dx} \).

- Tích phân chỉ phụ thuộc vào hàm số dưới dấu tích phân và các cận a, b mà không phụ thuộc vào biến x hay t, nghĩa là \(\int\limits_a^b {f(x)dx}  = \int\limits_a^b {f(t)dt} \).

- Ý nghĩa hình học của tích phân: Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = a, x = b là \(S = \int\limits_a^b {f(x)dx} \).

Ví dụ:

a) \(\int\limits_2^3 {3{x^2}dx}  = {x^3}\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. = {3^3} - {2^3} = 27 - 8 = 19\).

b) \(\int\limits_2^3 {{e^t}dt}  = {e^t}\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. = {e^1} - {e^0} = e - 1\).

2. Tính chất của tích phân

Ví dụ:

a) Cho \(\int\limits_0^2 {\sqrt {{e^x}} dx}  = 2(e - 1)\). Tính \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx} \).

Ta có \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx}  = \frac{1}{2}\int\limits_0^2 {\sqrt {{e^x}} dx}  = \frac{1}{2}.2(e - 1) = e - 1\).

b) Tính \(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx} \).

\(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx}  = 3\int\limits_0^{\frac{\pi }{2}} {\sin xdx}  - \int\limits_0^{\frac{\pi }{2}} {\cos xdx} \)

\( = ( - 3\cos x)\left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. - \sin \left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. =  - 3(0 - 1) - (1 - 0) = 2\).

c) Cho các hàm số f(x), g(x) liên tục trên đoạn [1;3] và \(\int\limits_1^2 {f(x)dx}  = \frac{1}{2}\), \(\int\limits_2^3 {f(x)dx}  = \frac{3}{2}\), \(\int\limits_1^3 {g(x)dx}  =  - 1\).

Ta có:

\(\int\limits_1^3 {f(x)dx}  = \int\limits_1^2 {f(x)dx}  + \int\limits_2^3 {f(x)dx}  = \frac{1}{2} + \frac{3}{2} = 2\).

\(\int\limits_1^3 {[2f(x) + g(x)]dx}  = 2\int\limits_1^3 {f(x)dx}  + \int\limits_1^3 {f(x)dx}  = 2.2 - 1 = 3\).

3. Tính tích phân trong một số trường hợp đơn giản

a) \(\int\limits_1^2 {{{(2x - 3)}^2}dx}  = \int\limits_1^2 {(4{x^2} - 12x + 9)dx}  = 4\int\limits_1^2 {{x^2}dx}  - 12\int\limits_1^2 {xdx}  + \int\limits_1^2 {9dx} \)

\( = \left( {\frac{4}{3}{x^3}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. - \left( {6{x^2}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. + (9x)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = \frac{1}{3}\).

b) \(\int\limits_{ - 1}^0 {{5^{2x - 1}}dx}  = \frac{1}{5}\int\limits_{ - 1}^0 {{5^{2x}}dx}  = \frac{1}{5}\int\limits_{ - 1}^0 {{{25}^x}dx}  = \frac{{{{25}^x}}}{{5\ln 25}}\left| {\begin{array}{*{20}{c}}0\\{ - 1}\end{array}} \right. = \frac{{24}}{{125\ln 25}}\).

c) \(\int\limits_{ - \frac{\pi }{4}}^0 {(2{{\tan }^2}x + 5)dx}  = \int\limits_{ - \frac{\pi }{4}}^0 {\left[ {2(1 + {{\tan }^2}x) + 3} \right]dx}  = 2\int\limits_{ - \frac{\pi }{4}}^0 {\frac{1}{{{{\cos }^2}x}}dx}  + \int\limits_{ - \frac{\pi }{4}}^0 {3dx} \)

\( = 2(\tan x)\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array} + (3x)} \right.\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array}} \right. = \frac{{3\pi  + 8}}{4}\).