Giải mục 2 trang 15, 16, 17, 18 SGK Toán 12 tập 2 - Cùng khám pháCho \(f(x) = 2x\). Tính và so sánh \(\int\limits_1^2 2 f(x){\mkern 1mu} dx\) và \(2\int\limits_1^2 f (x){\mkern 1mu} dx\). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
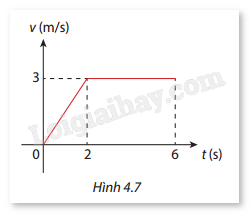
HĐ4 Trả lời câu hỏi Hoạt động 4 trang 15 SGK Toán 12 Cùng khám phá Cho \(f(x) = 2x\). Tính và so sánh \(\int\limits_1^2 2 f(x){\mkern 1mu} dx\) và \(2\int\limits_1^2 f (x){\mkern 1mu} dx\). Phương pháp giải: - Tính từng tích phân riêng biệt: \(\int\limits_1^2 2 f(x){\mkern 1mu} dx\) và \(2\int\limits_1^2 f (x){\mkern 1mu} dx\) - So sánh kết quả của hai tích phân. Lời giải chi tiết: Tính tích phân thứ nhất: \(\int\limits_1^2 2 f(x){\mkern 1mu} dx = \int\limits_1^2 2 (2x){\mkern 1mu} dx = \int\limits_1^2 4 x{\mkern 1mu} dx = \left[ {2{x^2}} \right]_1^2 = 2({2^2}) - 2({1^2}) = 8 - 2 = 6\) Tính tích phân thứ hai: \(2\int\limits_1^2 f (x){\mkern 1mu} dx = 2\int\limits_1^2 2 x{\mkern 1mu} dx = 2 \times \left[ {{x^2}} \right]_1^2 = 2 \times ({2^2} - {1^2}) = 2 \times (4 - 1) = 2 \times 3 = 6\) So sánh: \(\int\limits_1^2 2 f(x){\mkern 1mu} dx = 6\) và \(2\int\limits_1^2 f (x){\mkern 1mu} dx = 6\) Vậy, hai tích phân này bằng nhau. LT3 Trả lời câu hỏi Luyện tập 3 trang 15 SGK Toán 12 Cùng khám phá Cho \(\int\limits_1^4 {3\sqrt x } dx = 14\). Tính \(\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx\). Phương pháp giải: - Sử dụng tính chất của tích phân xác định để đơn giản hóa biểu thức. Chúng ta biết rằng: \(\int\limits_1^4 3 \sqrt x {\mkern 1mu} dx = 3\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx\) - Sử dụng giá trị đã cho \(\int\limits_1^4 {3\sqrt x } dx = 14\) để thiết lập phương trình và giải để tìm giá trị của \(\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx\). Lời giải chi tiết: Từ tính chất của tích phân xác định, ta có: \(\int\limits_1^4 3 \sqrt x {\mkern 1mu} dx = 3\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx\) Theo đề bài, ta biết rằng: \(3\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx = 14\) Chia cả hai vế của phương trình cho 3: \(\int\limits_1^4 {\sqrt x } {\mkern 1mu} dx = \frac{{14}}{3}\) HĐ5 Trả lời câu hỏi Hoạt động 5 trang 15 SGK Toán 12 Cùng khám phá Cho \(f(x) = 2x\), \(g(x) = 5\). Tính và so sánh: a) \(\int\limits_1^2 {\left[ {f(x) + g(x)} \right]} dx\) và \(\int\limits_1^2 f (x){\mkern 1mu} dx + \int\limits_1^2 g (x){\mkern 1mu} dx\). b) \(\int\limits_1^2 {\left[ {f(x) - g(x)} \right]} dx\) và \(\int\limits_1^2 f (x){\mkern 1mu} dx - \int\limits_1^2 g (x){\mkern 1mu} dx\). Phương pháp giải: - Tính từng tích phân riêng biệt bằng cách tìm nguyên hàm của \(f(x)\) và \(g(x)\) trên đoạn \([1;2]\). - Áp dụng tính chất của tích phân để so sánh kết quả của các biểu thức. Lời giải chi tiết: a) Tính tích phân: \(\int\limits_1^2 {\left[ {f(x) + g(x)} \right]} dx = \int\limits_1^2 {\left[ {2x + 5} \right]} dx\) Nguyên hàm của \(2x + 5\) là \({x^2} + 5x + C\): \(\int\limits_1^2 {\left[ {2x + 5} \right]} dx = \left[ {{x^2} + 5x} \right]_1^2 = \left[ {4 + 10} \right] - \left[ {1 + 5} \right] = 14 - 6 = 8\) Tính tích phân từng hàm riêng: \(\int\limits_1^2 f (x){\mkern 1mu} dx = \int\limits_1^2 2 x{\mkern 1mu} dx = \left[ {{x^2}} \right]_1^2 = 4 - 1 = 3\) \(\int\limits_1^2 g (x){\mkern 1mu} dx = \int\limits_1^2 5 {\mkern 1mu} dx = \left[ {5x} \right]_1^2 = 10 - 5 = 5\) So sánh: \(\int\limits_1^2 {\left[ {f(x) + g(x)} \right]} dx = 8\) \(\int\limits_1^2 f (x){\mkern 1mu} dx + \int\limits_1^2 g (x){\mkern 1mu} dx = 3 + 5 = 8\) Vậy \(\int\limits_1^2 {\left[ {f(x) + g(x)} \right]} dx = \int\limits_1^2 f (x){\mkern 1mu} dx + \int\limits_1^2 g (x){\mkern 1mu} dx\). b) Tương tự, tính tích phân trong phần b): \(\int\limits_1^2 {\left[ {f(x) - g(x)} \right]} dx = \int\limits_1^2 {\left[ {2x - 5} \right]} dx = \left[ {{x^2} - 5x} \right]_1^2 = \left[ {4 - 10} \right] - \left[ {1 - 5} \right] = - 6 + 4 = - 2\) So sánh: \(\int\limits_1^2 f (x){\mkern 1mu} dx - \int\limits_1^2 g (x){\mkern 1mu} dx = 3 - 5 = - 2\) Vậy \(\int\limits_1^2 {\left[ {f(x) - g(x)} \right]} dx = \int\limits_1^2 f (x){\mkern 1mu} dx - \int\limits_1^2 g (x){\mkern 1mu} dx\). LT4 Trả lời câu hỏi Luyện tập 4 trang 15 SGK Toán 12 Cùng khám phá Tính a) \(\int\limits_1^2 {\left( {4{x^3} - \frac{1}{{{x^2}}}} \right)dx} \); b) \(\int\limits_0^1 {(5 - 2{e^x})dx} \). Phương pháp giải: - Sử dụng các công thức tính nguyên hàm của các hàm số cơ bản: \(\int {{x^n}} dx = \frac{{{x^{n + 1}}}}{{n + 1}} + C,{\rm{ }}n \ne - 1\) \(\int {\frac{1}{{{x^n}}}} dx = \frac{{{x^{ - n + 1}}}}{{ - n + 1}} + C,n \ne 1\) \(\int {{e^x}} dx = {e^x} + C\) \(\int a dx = ax + C\) - Áp dụng tính chất số 2 của tích phân để tính. Lời giải chi tiết: a) Tìm nguyên hàm của \(4{x^3}\) và \( - \frac{1}{{{x^2}}}\): \(\int 4 {x^3}dx = 4 \cdot \frac{{{x^4}}}{4} = {x^4}\) \(\int - \frac{1}{{{x^2}}}dx = - \int {{x^{ - 2}}} dx = - \frac{{{x^{ - 1}}}}{{ - 1}} = \frac{1}{x}\) Vậy nguyên hàm của hàm số \(4{x^3} - \frac{1}{{{x^2}}}\) là: \(F(x) = {x^4} + \frac{1}{x}\) \(\int_1^2 {\left( {4{x^3} - \frac{1}{{{x^2}}}} \right)} dx = \left[ {{x^4} + \frac{1}{x}} \right]_1^2 = \left( {{2^4} + \frac{1}{2}} \right) - \left( {{1^4} + \frac{1}{1}} \right)\) \({2^4} = 16,\quad \frac{1}{2} = 0.5,\quad {1^4} = 1,\quad \frac{1}{1} = 1\) \(\int_1^2 {\left( {4{x^3} - \frac{1}{{{x^2}}}} \right)} dx = (16 + 0.5) - (1 + 1) = 16.5 - 2 = 14.5\) b) Tính nguyên hàm của 5 và \( - 2{e^x}\): \(\int 5 dx = 5x\) \(\int - 2{e^x}dx = - 2{e^x}\) Vậy nguyên hàm của hàm số \(5 - 2{e^x}\) là: \(F(x) = 5x - 2{e^x}\) Tính giá trị của tích phân tại cận từ 0 đến 1: \(\int_0^1 {\left( {5 - 2{e^x}} \right)} dx = \left[ {5x - 2{e^x}} \right]_0^1 = \left( {5 \cdot 1 - 2{e^1}} \right) - \left( {5 \cdot 0 - 2{e^0}} \right)\) \(5 \cdot 1 = 5,\quad {e^1} = e,\quad 5 \cdot 0 = 0,\quad {e^0} = 1\) \(\int_0^1 {\left( {5 - 2{e^x}} \right)} dx = (5 - 2e) - (0 - 2) = 5 - 2e + 2 = 7 - 2e\). HĐ6 Trả lời câu hỏi Hoạt động 6 trang 16 SGK Toán 12 Cùng khám phá Cho \(f(x) = 2x\). Tính và so sánh \(\int\limits_1^2 {f(x)dx} + \int\limits_2^3 {f(x)} dx\) và \(\int\limits_1^3 {f(x)} dx\). Phương pháp giải: Sử dụng các công thức tính tích phân của hàm số cơ bản để tính các tích phân riêng lẻ, sau đó cộng lại và so sánh với tích phân từ cận nhỏ nhất đến cận lớn nhất. Lời giải chi tiết: Tính nguyên hàm của $f(x) = 2x$: \(F(x) = \int 2 xdx = {x^2}\) Tính các tích phân: \(\int_1^2 2 xdx = \left[ {{x^2}} \right]_1^2 = {2^2} - {1^2} = 4 - 1 = 3\) \(\int_2^3 2 xdx = \left[ {{x^2}} \right]_3^2 = {\left( 3 \right)^2} - {2^2} = 9 - 4 = 5\) \(\int_1^3 2 xdx = \left[ {{x^2}} \right]_1^3 = {3^2} - {1^2} = 9 - 1 = 8\) So sánh: \(\int_1^2 2 xdx + \int_2^3 2 xdx = 3 + 5 = 8\) \(\int_1^2 f (x)dx + \int_2^3 f (x)dx = 8\) \(\int_1^3 f (x)dx = 8\) Do đó, hai tích phân này bằng nhau. LT5 Trả lời câu hỏi Luyện tập 5 trang 17 SGK Toán 12 Cùng khám phá a) Cho hàm số \(f(x)\) liên tục trên đoạn \([ - 1;5]\) và \[\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = 12\]. Tính \(\int_{ - 1}^5 f (x)dx\). b) Cho \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^3} + 2}&{{\rm{khi }}x > - 1}\\{2x + 3}&{{\rm{khi }}x \le - 1}\end{array}} \right.\). Tính \(\int_{ - 2}^1 f (x)dx\). Phương pháp giải: a) Sử dụng tính chất của tích phân và giả thiết đã cho, ta tách tích phân \[\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx\] thành hai phần: \(\int_{ - 1}^5 2 x{\mkern 1mu} dx\) và \( - 3\int_{ - 1}^5 f (x){\mkern 1mu} dx\). Sau đó, chúng ta tính từng tích phân riêng lẻ và giải phương trình để tìm \(\int_{ - 1}^5 f (x)dx\). b) Đối với bài này, ta chia tích phân \(\int_{ - 2}^1 f (x)dx\) thành hai phần dựa trên định nghĩa của hàm \(f(x)\). Tính tích phân riêng trên từng đoạn sau đó cộng kết quả lại. Lời giải chi tiết: a) Sử dụng giả thiết\(\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = 12\): \(\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = \int_{ - 1}^5 2 x{\mkern 1mu} dx + - 3\int_{ - 1}^5 f (x){\mkern 1mu} dx = 12\) Tính \(\int_{ - 1}^5 2 x{\mkern 1mu} dx\): \(\int_{ - 1}^5 2 x{\mkern 1mu} dx = \left. {{x^2}} \right|_{ - 1}^5 = {5^2} - {( - 1)^2} = 25 - 1 = 24\) Thay vào phương trình: \(24 - 3\int_{ - 1}^5 f (x){\mkern 1mu} dx = 12\) \(3\int_{ - 1}^5 f (x){\mkern 1mu} dx = 12\) \(\int_{ - 1}^5 f (x){\mkern 1mu} dx = 4\) b) Chia tích phân thành hai phần dựa trên định nghĩa của hàm \(f(x)\): \(\int_{ - 2}^1 f (x)dx = \int_{ - 2}^{ - 1} f (x)dx + \int_{ - 1}^1 f (x)dx\) Tính \(\int_{ - 2}^{ - 1} {(2x + 3)} dx\): \(\int_{ - 2}^{ - 1} {(2x + 3)} dx = \left. {({x^2} + 3x)} \right|_{ - 2}^{ - 1} = [{( - 1)^2} + 3( - 1)] - [{( - 2)^2} + 3( - 2)] = - 2 + 2 = 0\) Tính \(\int_{ - 1}^1 {({x^3} + 2)} dx\): \(\int_{ - 1}^1 {({x^3} + 2)} dx = \left. {\left( {\frac{{{x^4}}}{4} + 2x} \right)} \right|_{ - 1}^1 = \left[ {\frac{1}{4} + 2} \right] - \left[ {\frac{1}{4} - 2} \right] = 4\) Vậy \(\int_{ - 2}^1 f (x)dx = 0 + 4 = 4\). VD2 Trả lời câu hỏi Vận dụng 2 trang 18 SGK Toán 12 Cùng khám phá Hình 4.7 là đồ thị vận tốc \(v(t)\) của một vật (t = 0 là thời điểm vật bắt đầu chuyển động). a) Viết công thức của hàm số \(v(t)\) với \(t \in [0;6]\). b) Tính quãng đường vật di chuyển được trong 6 giây đầu tiên.
Phương pháp giải: a) Dựa trên đồ thị, ta xác định công thức của hàm số \(v(t)\) theo từng đoạn thời gian khác nhau. b) Để tính quãng đường di chuyển, ta tính diện tích dưới đường cong của đồ thị vận tốc trong khoảng thời gian đã cho. Lời giải chi tiết: a) Hàm số \(v(t)\) được chia thành hai đoạn dựa trên đồ thị: \(v(t) = \left\{ {\begin{array}{*{20}{l}}{\frac{3}{2}t}&{{\rm{khi }}0 \le t \le 2}\\3&{{\rm{khi }}2 < t \le 6}\end{array}} \right.\) b) Quãng đường vật di chuyển được trong 6 giây đầu tiên là diện tích dưới đồ thị của hàm \(v(t)\) từ 0 đến 6: \(S = \int_0^2 {\frac{3}{2}} t{\mkern 1mu} dt + \int_2^6 3 {\mkern 1mu} dt\) Tính \(\int_0^2 {\frac{3}{2}} t{\mkern 1mu} dt\): \(\int_0^2 {\frac{3}{2}} t{\mkern 1mu} dt = \left. {\frac{3}{4}{t^2}} \right|_0^2 = \frac{3}{4}({2^2}) = 3\) Tính \(\int_2^6 3 {\mkern 1mu} dt\): \(\int_2^6 3 {\mkern 1mu} dt = \left. {3t} \right|_2^6 = 3(6 - 2) = 12\) Vậy tổng quãng đường là: \(S = 3 + 12 = 15{\mkern 1mu} {\rm{m}}\).
|




















Danh sách bình luận