Lý thuyết Phương trình mặt cầu Toán 12 Cánh Diều1. Định nghĩa mặt cầu Quảng cáo
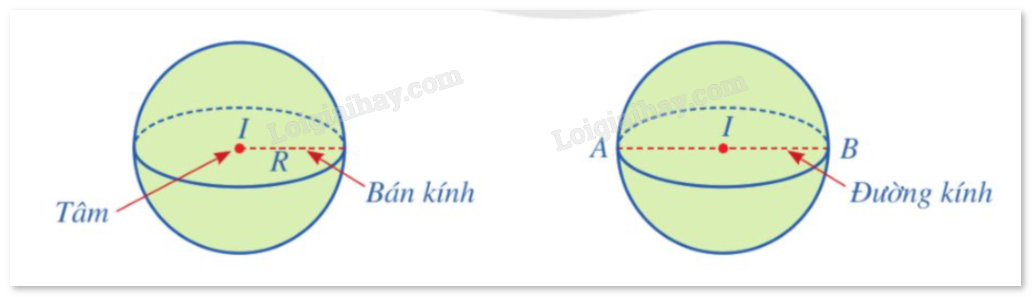
1. Định nghĩa mặt cầu
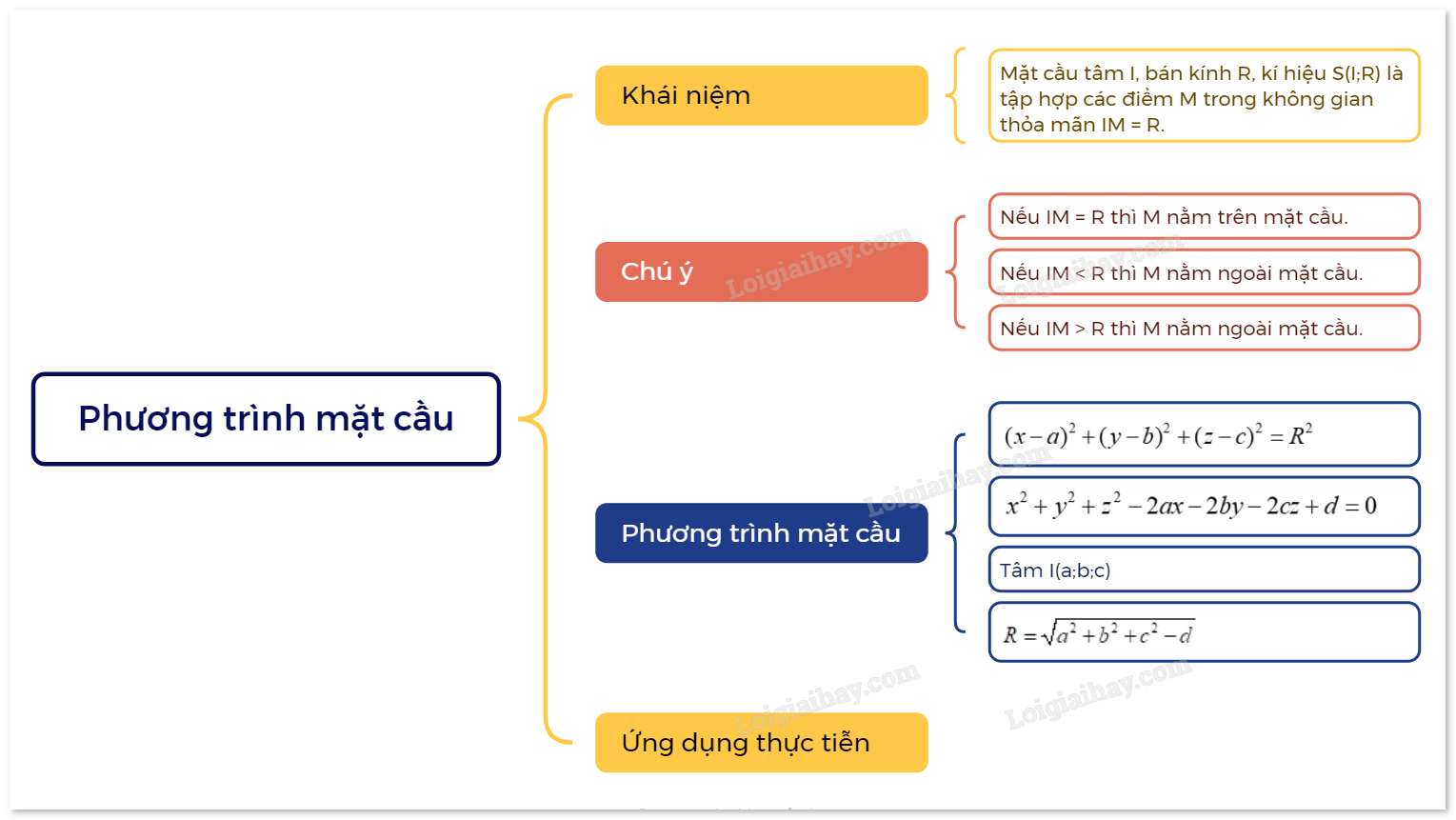
Nhận xét: Cho mặt cầu S(I;R). - Nếu IM = R thì M nằm trên mặt cầu. - Nếu IM < R thì M nằm ngoài mặt cầu. - Nếu IM > R thì M nằm ngoài mặt cầu. Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu tâm I(-2; 1; 5) bán kính 3. Các điểm A(10; 1; 2), B(0; 1; 4), C(0; 3; 4) nằm trong, nằm trên hay nằm ngoài mặt cầu đó? Giải: Do \(IA = \sqrt {{{\left( {10 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}} = \sqrt {153} > 3\) nên điểm A(10; 1; 2) nằm ngoài mặt cầu đó. Do \(IB = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 5 < 3\) nên điểm B(0; 1; 4) nằm trong mặt cầu đó. Do \(IC = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 9 = 3\) nên điểm C(0; 3; 4) nằm trên mặt cầu đó. 2. Phương trình mặt cầu
Ví dụ 1: Viết phương trình mặt cầu, biết: a) Có tâm I(1; 2; 3), bán kính R = 10. b) Có tâm I(3; -1; -5) và đi qua điểm B(0; 2; 1). Giải: a) Phương trình của mặt cầu tâm I(1; 2; 3) bán kính R = 10 là \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 100\). b) Bán kính mặt cầu là \(R = IB = \sqrt {{{(0 - 3)}^2} + {{(2 + 1)}^2} + {{(1 + 5)}^2}} = \sqrt {54} \). Phương trình mặt cầu tâm I(3;-1;-5) bán kính \(R = \sqrt {54} \) là \({(x - 3)^2} + {(y + 1)^2} + {(z + 5)^3} = 54\). Nhận xét: Cho mặt cầu tâm I(a; b; c) bán kính R có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\). Ta có thể viết phương trình đó dưới dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\), với \(d = {a^2} + {b^2} + {c^2} - {R^2}\). Dạng phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) xác định một mặt cầu khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\) với tâm I(a;b;c) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \). Ví dụ 2: Mỗi phương tình sau có là phương trình mặt cầu hay không? Vì sao? a) \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\). b) \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\). Giải: a) Phương trình \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\) không phải phương trình mặt cầu vì hệ số của \({x^2}\) và \({y^2}\) khác nhau. b) Phương trình \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\) không phải phương trình mặt cầu vì không có biểu thức \({z^2}\). Ví dụ 3: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó. a) \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\). b) \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\). Giải: a) Phương trình \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = 2;b = - 5;c = 1;d = 14\). Ta có \({a^2} + {b^2} + {c^2} - d = 4 + 25 + 1 - 14 = 16 > 0\). Suy ra phương trình đã cho là phương trình mặt cầu tâm I(2;-5;1), bán kính R = 4. b) Phương trình \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - 1;b = - 2;c = 3;d = 20\). Ta có \({a^2} + {b^2} + {c^2} - d = 1 + 4 + 9 - 20 = - 6 < 0\). Suy ra phương trình đã cho không phải phương trình mặt cầu. 2. Vận dụng của phương trình mặt cầu Phương trình mặt cầu có nhiều ứng dụng trong thực tiễn như thiết kế xây dựng, tính toán các yếu tố kĩ thuật,… Ví dụ: Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là kilomet), một trạm thu phát sóng điện thoại di động được đặt ở vị trí I(−3; 2; 7). a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài của vùng phủ sóng trong không gian, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là 3 km. b) Điểm A(−2; 1; 8) nằm trong hay nằm ngoài mặt cầu đó? Nếu người dùng điện thoại ở điểm A(−2; 1; 8) có thể sử dụng dịch vụ của trạm này hay không? c) Điểm B(2; 3; 4) nằm trong hay nằm ngoài mặt cầu đó? Nếu người dùng điện thoại ở điểm B(2; 3; 4) có thể sử dụng dịch vụ của trạm này hay không? Giải: a) Phương trình mặt cầu để mô tả ranh giới bên ngoài của vùng phủ sóng trong không gian là: \({(x + 3)^2} + {(y - 2)^2} + {(z - 7)^2} = 9\). b) Ta có: \(IA = \sqrt {{{\left( { - 2 - ( - 3)} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {{\left( {8 - 7} \right)}^2}} = \sqrt 3 < 3\). Vì IA < R nên điểm A nằm trong mặt cầu. Vậy người dùng điện thoại ở điểm A(−2;1;8) có thể sử dụng dịch vụ của trạm này. c) Ta có: \(IB = \sqrt {{{\left( { - 2 - ( - 3)} \right)}^2} + {{\left( {3 - 2} \right)}^2} + {{\left( {4 - 7} \right)}^2}} = \sqrt {35} > 3\). Vì IB > R nên điểm B nằm ngoài mặt cầu. Vậy người dùng điện thoại ở điểm B(2;3;4) không thể sử dụng dịch vụ của trạm này.
|




















Danh sách bình luận