Lý thuyết Phương trình bậc nhất hai ẩn.Phương trình bậc nhất hai ẩn x, y là hệ thức dạng: Quảng cáo
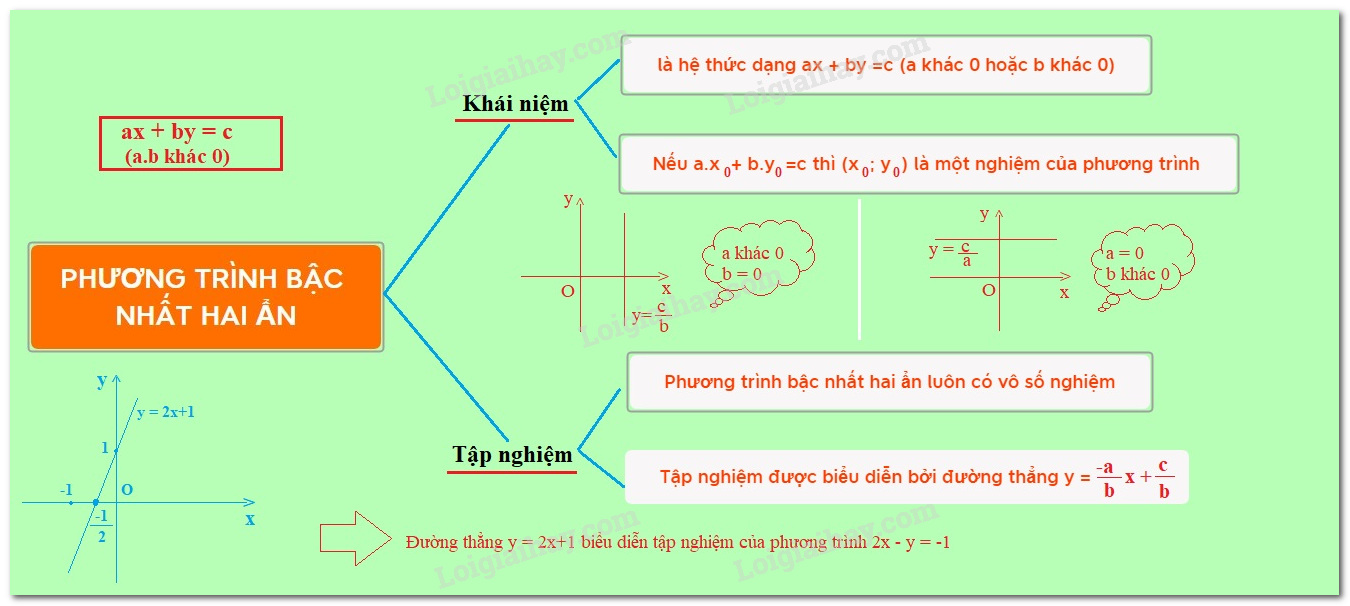
1. Các kiến thức cần nhớ Khái niệm phương trình bậc nhất hai ẩn +) Phương trình bậc nhất hai ẩn là phương trình có dạng $ax + by = c$ Trong đó $a,b,c$ là những số cho trước $a \ne $$0$ hoặc $b \ne 0$ . - Nếu các số thực ${x_0},\,{y_0}$ thỏa mãn $ax + by = c$ thì cặp số $({x_0},\,{y_0})$ được gọi là nghiệm của phương trình $ax + by = c$. - Trong mặt phẳng tọa độ $Oxy$ , mỗi nghiệm $({x_0},\,{y_0})$ của phương trình $ax + by = c$ được biểu diễn bới điểm có tọa độ $({x_0},\,{y_0})$. Tập nghiệm của phương trình bậc nhất hai ẩn Phương trình bậc nhất hai ẩn $ax + by = c$ luôn có vô số nghiệm. Tập nghiệm của phương trình được biểu diễn bởi đường thẳng $d:ax + by = c.$ +) Nếu $a \ne 0$ và $b = 0$ thì phương trình có nghiệm $\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.$ và đường thẳng $d$ song song hoặc trùng với trục tung. +) Nếu $a = 0$ và $b \ne 0$ thì phương trình có nghiệm $\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.$ và đường thẳng $d$ song song hoặc trùng với trục hoành. +) Nếu $a \ne 0$ và $b \ne 0$ thì phương trình có nghiệm $\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.$ và đường thẳng $d$ là đồ thị hàm số $y = - \dfrac{a}{b}x + \dfrac{c}{b}$ 2. Các dạng toán thường gặp Dạng 1: Tìm điều kiện của tham số để một cặp số cho trước là nghiệm của phương trình bậc nhất hai ẩn. Phương pháp: Nếu cặp số thực $({x_0},\,{y_0})$thỏa mãn $ax + by = c$ thì nó được gọi là nghiệm của phương trình $ax + by = c$. Dạng 2: Viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn. Biểu diễn tập nghiệm trên hệ trục tọa độ. Phương pháp: Xét phương trình bậc nhất hai ẩn $ax + by = c$. 1. Để viết công thức nghiệm tổng quát của phương trình, trước tiên ta biểu diễn $x$ theo $y$ ( hoặc $y$ theo $x$) rồi đưa ra công thức nghiệm tổng quát. 2. Để biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có phương trình $ax + by = c$. Dạng 3: Tìm điều kiện của tham số để đường thẳng $ax + by = c$ thỏa mãn điều kiện cho trước Phương pháp: Ta có thể sử dụng một số lưu ý sau đây khi giải dạng toán này: 1. Nếu \(a \ne 0\) và \(b = 0\) thì phương trình đường thẳng $d: ax + by = c$ có dạng $d:x = \dfrac{c}{a}$. Khi đó $d$ song song hoặc trùng với $Oy$ . 2. Nếu \(a = 0\) và \(b \ne 0\) thì phương trình đường thẳng $d: ax + by = c$ có dạng $d:y = \dfrac{c}{b}$. Khi đó $d$ song song hoặc trùng với $Ox$ . 3. Đường thẳng $d:ax + by = c$ đi qua điểm $M({x_0},\,{y_0})$ khi và chỉ khi $a{x_0} + b{y_0} = c$. Dạng 4: Tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn Phương pháp: Để tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn $ax + by = c$, ta làm như sau: Cách 1: Bước 1: Rút gọn phương trình, chú ý đến tính chia hết của các ẩn Cách 2: Bước 1. Tìm một nghiệm nguyên $({x_0},\,{y_0})$ của phương trình. Bước 2. Đưa phương trình về dạng $a(x - {x_0}) + b(y - {y_0}) = 0$ từ đó dễ dàng tìm được các nghiệm nguyên của phương trình đã cho.
|





















Danh sách bình luận