Lý thuyết Hệ hai phương trình bậc nhất hai ẩn.

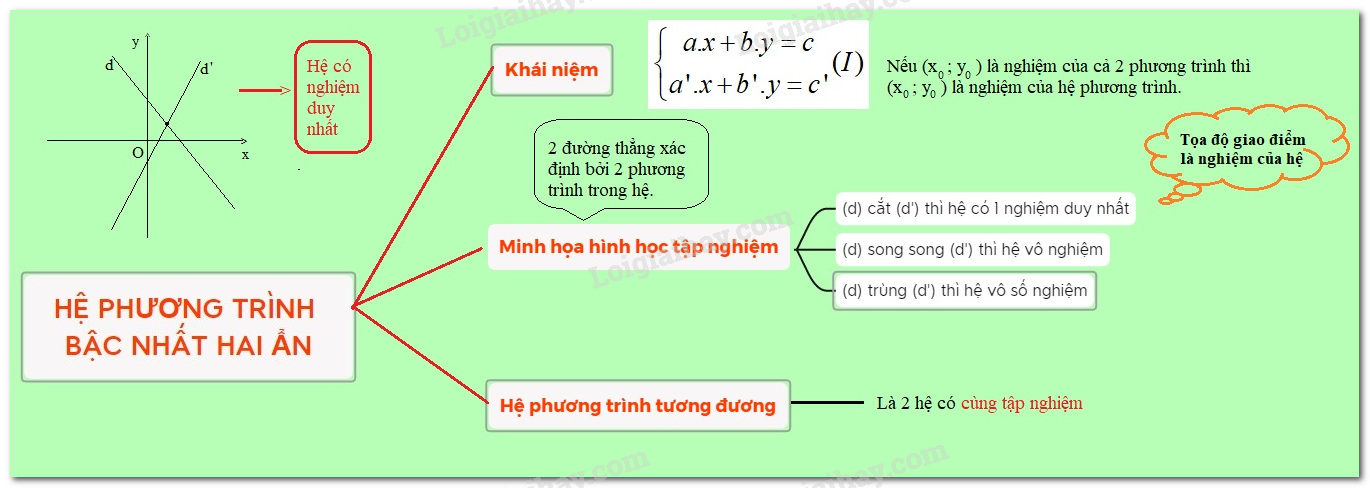
1. Các kiến thức cần nhớ

Khái niệm hệ phương trình bậc nhất hai ẩn

- Hệ phương trình bậc nhất hai ẩn là hệ phương trình có dạng:

$\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,\,(2)\end{array} \right.$

Trong đó $a, b, c, a’, b’, c’$ là các số thực cho trước, $x$ và $y$ là ẩn số

- Nếu hai phương trình (1) và (2) có nghiệm chung $({x_0},\,{y_0})$thì$({x_0},\,{y_0})$ được gọi là nghiệm của hệ phương trình. Nếu hai phương trình (1) và (2) không có nghiệm chung thì hệ phương trình vô nghiệm.

- Giải hệ phương trình là tìm tất cả các nghiệm của nó.

Hai hệ phương trình được gọi là tương đương  nếu chúng có cùng tập nghiệm

Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn

Hệ phương trình có nghiệm duy nhất \( \Leftrightarrow \dfrac{a}{{a'}} \ne \dfrac{b}{{b'}};\)

Hệ phương trình vô nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} \ne \dfrac{c}{{c'}}\);

Hệ phương trình có vô số nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{c}{{c'}}.\)

2. Các dạng toán thường gặp

Dạng 2: Kiểm tra cặp số cho trước có là nghiệm của hệ phương trình bậc nhất hai ẩn hay không?

Phương pháp:

Cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) khi và chỉ khi nó thỏa mãn cả hai phương trình của hệ.

Dạng 3: Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp đồ thị

Phương pháp:

Để giải hệ phương trình bậc nhất hai ẩn $\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.$ bằng phương pháp đồ thị ta làm như sau:

Bước 1. Vẽ hai đường thẳng \(d:ax + by = c\) và \(d':a'x + b'y = c'\) trên cùng một hệ trục tọa độ. Hoặc tìm tọa độ giao điểm của hai đường thẳng.

Bước 2. Xác định nghiệm của hệ phương trình dựa vào đồ thị đã vẽ ở bước 1 (hay nghiệm của hệ phương trình chính là tọa độ giao điểm của hai đường thẳng)