Lý thuyết Các quy tắc tính xác suất Toán 12 Cùng khám phá

1. Công thức xác suất toàn phần

Ví dụ 1: Người ta khảo sát khả năng chơi nhạc cụ của một nhóm học sinh tại trường X. Nhóm này có 60% học sinh là nam. Kết quả khảo sát cho thấy 20% học sinh nam và 15% học sinh nữ biết chơi ít nhất một nhạc cụ.
Chọn ngẫu nhiên một sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ.

Giải:

Xét phép thử chọn ngẫu nhiên một học sinh trong nhóm.

Gọi A là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và B, \(\overline B \) lần lượt là các biến cố "Chọn được học sinh nam" và "Chọn được một học sinh nữ".

Theo đề bài: \(P\left( B \right) = 60\%  = 0,6\); \(P\left( {\overline B } \right) = 1 - 0,6 = 0,4\);

\(P(A\mid B) = 20\%  = 0,2\); \(P(A\mid \overline B ) = 15\%  = 0,15.\)

Áp dụng công thức xác suất toàn phần, ta có:

\(P\left( A \right) = P\left( B \right) \cdot P(A\mid B) + P\left( {\overline B } \right) \cdot P(A\mid \overline B ) = 0,6 \cdot 0,2 + 0,4 \cdot 0,15 = 0,18.\)

Vậy xác suất để chọn được một học sinh biết chơi nhạc cụ là 0,18 hay 18%.

Ví dụ 2: Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 viên bi đỏ và 5 viên bi xanh, hộp thứ hai chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ.

Giải:

Cách 1:

Gọi:

A là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";

B là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ";

\(\overline B \) là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh".

Ta có: \(P\left( B \right) = \frac{5}{{10}} = \frac{1}{2}\); \(P\left( {\overline B } \right) = \frac{5}{{10}} = \frac{1}{2}\).

Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ thì sau khi chuyển, hộp thứ hai có 7 bi đỏ và 4 bi xanh. Do đó \(P(A\mid B) = \frac{7}{{11}}\).

Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh thì sau khi chuyển, hộp thứ hai có 6 bi đỏ và 5 bi xanh. Do đó \(P(A\mid \overline B ) = \frac{6}{{11}}\).

Áp dụng công thức xác suất toàn phần, ta có:

\(P\left( A \right) = P\left( B \right) \cdot P(A\mid B) + P\left( {\overline B } \right) \cdot P(A\mid \overline B ) = \frac{1}{2} \cdot \frac{7}{{11}} + \frac{1}{2} \cdot \frac{6}{{11}} = \frac{{13}}{{22}}\).

Vậy xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ bằng \(\frac{{13}}{{22}}\).

Cách 2:

Gọi:

A là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";

C là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi của hộp thứ nhất";

\(\overline C \) là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi của hộp thứ hai".

Sau khi chuyển một viên bi từ hộp thứ nhất sang hộp thứ hai thì hộp thứ hai có 11 viên bi.

Ta có: \(P\left( C \right) = \frac{1}{{11}}\); \(P\left( {\overline C } \right) = \frac{{10}}{{11}}\).

Xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ của hộp thứ nhất: \(P(A\mid C) = \frac{5}{{10}} = \frac{1}{2}\).

Xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ của hộp thứ hai: \(P(A\mid \overline C ) = \frac{6}{{10}} = \frac{3}{5}\).

Áp dụng công thức xác suất toàn phần, ta có:

\(P\left( A \right) = P\left( C \right) \cdot P(A\mid C) + P\left( {\overline C } \right) \cdot P(A\mid \overline C ) = \frac{1}{{11}} \cdot \frac{1}{2} + \frac{{10}}{{11}} \cdot \frac{3}{5} = \frac{{13}}{{22}}\).

Vậy xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ bằng \(\frac{{13}}{{22}}\).

2. Công thức Bayes

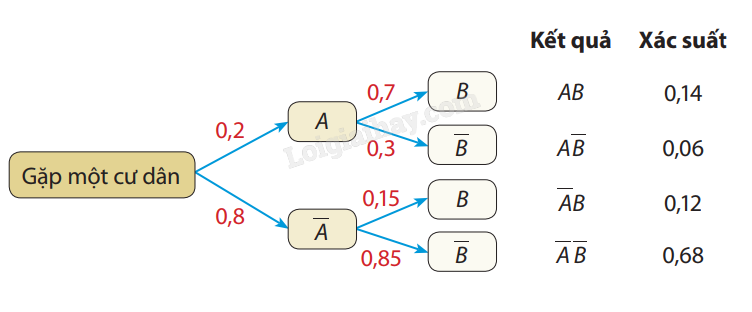
Lưu ý: Do \(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )\) nên công thức Bayes còn có dạng \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(B).P(A|B) + P(\overline B ).P(A|\overline B )}}\).

Ví dụ 1: Cho hai biến cố A, B sao cho P(A) = 0,6; P(B) = 0,4; P(A|B) = 0,3. Tính P(B|A).

Giải:

Áp dụng công thức Bayes, ta có: \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}} = \frac{{0,4.0,3}}{{0,6}} = 0,2\).

Ví dụ 2: Kết quả khảo sát tại một xã cho thấy có 20% cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khỏe về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là 70%, 15%.

a) Nếu ta gặp một cư dân của xã thì xác suất người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp là bao nhiêu?

b) Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khỏe về đường hô hấp thì xác suất người đó có hút thuốc lá là bao nhiêu?

Giải:

Giả sử ta gặp một cư dân của xã, gọi A là biến cố "Người đó có hút thuốc lá" và B là biến cố "Người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp". Ta có sơ đồ hình cây sau:

a) Ta có: \(P\left( B \right) = P\left( A \right).P(B\mid A) + P\left( {\overline A } \right).P(B\mid \overline A ) = 0,14 + 0,12 = 0,26.\)

Vậy nếu ta gặp một cư dân của xã thì xác suất người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp là 26%.

b) Theo công thức Bayes, ta có: \(P(A\mid B) = \frac{{P\left( A \right)P(B\mid A)}}{{P\left( B \right)}} = \frac{{0,14}}{{0,26}} \approx 0,54.\)
Vậy nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khỏe về đường hô hấp thì xác suất người đó có hút thuốc lá là khoảng 54%.