Luyện tập 7 trang 172 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Chứng minh rằng tổng hai khoảng cách từ một điềm trên cạnh đáy của một tam giác cân đến hai cạnh bên luôn bẳng chiều cao ứng với cạnh bên. Quảng cáo
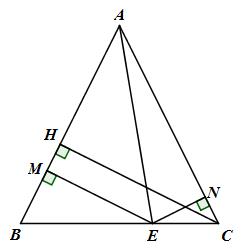
Đề bài Chứng minh rằng tổng hai khoảng cách từ một điềm trên cạnh đáy của một tam giác cân đến hai cạnh bên luôn bẳng chiều cao ứng với cạnh bên. Lời giải chi tiết Kẻ \(EM \bot AB\) tại M, \(EN \bot AC\) tại N \(EM + EN\) là tổng hai khoảng cách cần xét. Ta có: \({S_{ABC}} = {S_{ABE}} + {S_{ACE}} = {1 \over 2}AB.ME + {1 \over 2}C.NE\) Mà \(AB = AC\,\,(\Delta ABC\) cân tại A) Nên \({S_{ABC}} = {1 \over 2}AB.ME + {1 \over 2}AB.NE = {1 \over 2}AB\left( {ME + NE} \right)\) Mặt khác \({S_{ABC}} = {1 \over 2}AB.CH\) Do đó \({1 \over 2}AB\left( {ME + NE} \right) = {1 \over 2}AB.CH \Rightarrow ME + NE = CH\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
