Luyện tập 10 trang 172 Tài liệu dạy – học Toán 8 tập 1

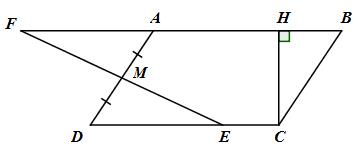
Đề bài

Cho hình bình hành ABCD có M là trung điểm của AD và E là một điểm tuỳ ý trên đoạn CD. Đường thẳng EM căt AB tại F. Hãy so sánh diện tích cùa hình bình hành ABCD và tứ giác ECBF.

Lời giải chi tiết

Xét \(\Delta AMF\) và \(\Delta MED\) có:

\(MA = MD\)  (M là trung điểm của AD)

\(\widehat {AMF} = \widehat {DME}\) (hai góc đối đỉnh)

\(\widehat {FAM} = \widehat {MDE}\) (hai góc so le trong và \(AF // DE\))

Do đó \(\Delta AMF = \Delta DME\,\left( {g.c.g} \right)\)

Tứ giác ECBF có :

EC // BF (DC // AB, \(E \in CD,\,\,F \in BA\)) \( \Rightarrow \) Tứ giác ECBF là hình thang

Kẻ \(CH \bot AB\) tại H

\({S_{ECBF}} = {1 \over 2}CH\left( {EC + BF} \right) = {1 \over 2}CH\left( {EC + AF + AB} \right)\),

Mà \(AF = DE\,\,\left( {\Delta AMF = \Delta DME} \right)\)

Và \(AB = CD\) (ABCD là hình bình hành)

Nên \({S_{ECBF}} = {1 \over 2}CH\left( {EC + DE + CD} \right) = {1 \over 2}CH\left( {CD + CD} \right) = {1 \over 2}CH.2CD = CH.CD = {S_{ABCD}}\)

Loigiaihay.com