Luyện tập 6 trang 172 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho tam giác đều ABC có cạnh là a. Chứng minh rằng tổng các khoảng cách từ một điếm M bên trong tam giác đến ba cạnh luôn bằng \({{a\sqrt 3 } \over 2}\) .

Lời giải chi tiết

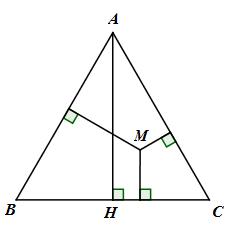
Kẻ đường cao AH của tam giác ABC.

\(\Delta ABC \Rightarrow \) AH là đường trung tuyến của tam giác ABC \( \Rightarrow H\) là trung điểm của BC

\( \Rightarrow BH = {{BC} \over 2} = {a \over 2}\)

Tam giác ABH vuông tại H \( \Rightarrow A{H^2} + B{H^2} = A{B^2}\) (định lí Pytago)

\( \Rightarrow A{H^2} + {{{a^2}} \over 4} = {a^2} \Rightarrow AH = {{a\sqrt 3 } \over 2}\)

Gọi m, n, p lần lượt là khoảng cách từ M đến AB, AC, BC

Ta có: \({S_{ABC}} = {S_{ABM}} + {S_{ACM}} + {S_{BCM}} = {1 \over 2}.m.a + {1 \over 2}.n.a + {1 \over 2}.p.a = {1 \over 2}a\left( {m + n + p} \right)\)

Mặt khác: \({S_{ABC}} = {1 \over 2}AH.BC = {1 \over 2}{{a\sqrt 3 } \over 2}.a\)

\( \Rightarrow {1 \over 2}.a.\left( {m + n + p} \right) = {1 \over 2}.{{a\sqrt 3 } \over 2}.a \Rightarrow m + n + p = {{a\sqrt 3 } \over 2}\)

Vậy ta có điều phải chứng minh.

Loigiaihay.com