Hoạt động 9 trang 83 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Cho hai tam giác vuông MNP và ABC có kích thước như hình 25 Quảng cáo
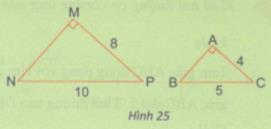
Đề bài Cho hai tam giác vuông MNP và ABC có kích thước như hình 25. Tính các tỉ số \({{AC} \over {MP}}\) và \({{AB} \over {MN}}\) . Tam giác MNP có đồng dạng với tam giác ABC không ? Vì sao ? Lời giải chi tiết \({{AC} \over {MP}} = {4 \over 8} = {1 \over 2}\) ∆MNP vuông tại M \( \Rightarrow M{N^2} + M{P^2} = N{P^2}\) (định lí Py-ta-go) Do đó \(M{N^2} = N{P^2} - M{P^2} \) \(= {10^2} - {8^2} = 36,\) \(MN > 0 \Rightarrow MN = \sqrt {36} = 6\) ∆ABC vuông tại A \( \Rightarrow A{B^2} + A{C^2} = B{C^2}\) (định lí Py-ta-go) \( \Rightarrow A{B^2} = B{C^2} - A{C^2} = {5^2} - {4^2} = 9\) \(AB > 0 \Rightarrow AB = \sqrt 9 = 3\) Ta có \({{AB} \over {MN}} = {3 \over 6} = {1 \over 2}\) Xét ∆ABC và ∆MNP có \({{AB} \over {MN}} = {{AC} \over {MP}},\widehat A = \widehat M( = 90^\circ ) \) \(\Rightarrow \Delta ABC \sim \Delta MNP(c.g.c)\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
