Giải phần A. Tái hiện, củng cố trang 12 Bài tập phát triển năng lực Toán 4 tập 2Rút gọn các phân số theo mẫu (theo mẫu) .... Điền dấu (>; <; =) thích hợp vào ô trống: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Rút gọn các phân số theo mẫu (theo mẫu): Phương pháp giải: Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1. - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết:
Câu 2 Quy đồng mẫu số các phân số: a) \(\frac{9}{7}\) và $\frac{8}{5}$ b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$ c) \(\frac{5}{{22}}\) và $\frac{7}{{33}}$ d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$ Phương pháp giải: - Tìm mẫu số chung - Tìm thừa số phụ bằng cách lấy mẫu số chung chia cho mẫu số của mỗi phân số - Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ vừa tìm được. Lời giải chi tiết: a) \(\frac{9}{7}\) và $\frac{8}{5}$ Ta có $\frac{9}{7} = \frac{{9 \times 5}}{{7 \times 5}} = \frac{{45}}{{35}}$ ; \(\frac{8}{5} = \frac{{8 \times 7}}{{5 \times 7}} = \frac{{56}}{{35}}\) Vậy quy đồng mẫu số của \(\frac{9}{7}\) và $\frac{8}{5}$ được \(\frac{{45}}{{35}}\) và $\frac{{56}}{{35}}$. b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$ Ta có: \(\frac{5}{{18}} = \frac{{5 \times 5}}{{18 \times 5}} = \frac{{25}}{{90}}\) ; \(\frac{9}{{10}} = \frac{{9 \times 9}}{{10 \times 9}} = \frac{{81}}{{90}}\) Vậy quy đồng mẫu số của$\frac{5}{{18}}$ và $\frac{9}{{10}}$ được \(\frac{{25}}{{90}}\) và $\frac{{81}}{{90}}$. c) \(\frac{5}{{22}}\) và $\frac{7}{{33}}$ Ta có $\frac{5}{{22}} = \frac{{5 \times 3}}{{22 \times 3}} = \frac{{15}}{{66}}$ ; \(\frac{7}{{33}} = \frac{{7 \times 2}}{{33 \times 2}} = \frac{{14}}{{66}}\) Vậy quy đồng mẫu số của \(\frac{5}{{22}}\) và $\frac{7}{{33}}$ được \(\frac{{15}}{{66}}\) và $\frac{{14}}{{66}}$. d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$ Ta có $\frac{3}{{12}} = \frac{{3 \times 5}}{{12 \times 5}} = \frac{{15}}{{60}}$ ; \(\frac{7}{{20}} = \frac{{7 \times 3}}{{20 \times 3}} = \frac{{21}}{{60}}\) Vậy quy đồng mẫu số của $\frac{3}{{12}}$ và $\frac{7}{{20}}$được \(\frac{{15}}{{60}}\) và $\frac{{21}}{{60}}$. Câu 3 Điền dấu (>; <; =) thích hợp vào ô trống:
Phương pháp giải: Trong hai phân số có cùng mẫu số: +) Phân số nào có tử số bé hơn thì phân số đó bé hơn. +) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn. +) Nếu tử số bằng nhau thì hai phân số đó bằng nhau. Lời giải chi tiết:
Câu 4 Điền dấu (>; <; =) thích hợp vào ô trống:
Phương pháp giải: Bước 1: Quy đồng mẫu số hai phân số. Bước 2: So sánh hai phân số có cùng mẫu số đó. Bước 3: Rút ra kết luận. Lời giải chi tiết:
Câu 5 Điền dấu (>; <; =) thích hợp vào ô trống:
Phương pháp giải: - Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn. - Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới. Lời giải chi tiết:
|














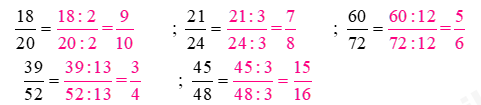


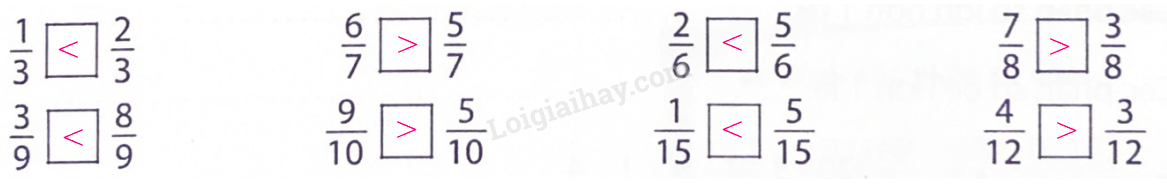

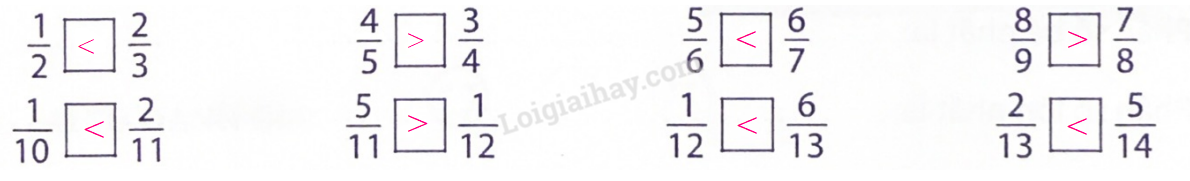







Danh sách bình luận