Giải mục 4 trang 43, 44, 45 Chuyên đề học tập Toán 10 - Cánh diềuGiả sử đường elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(0 < c < a\). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
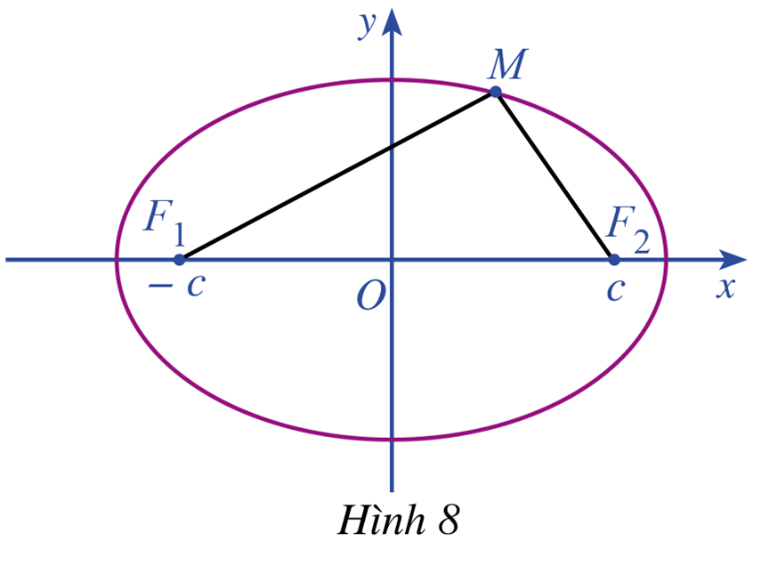
HĐ 5 Giả sử đường elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(0 < c < a\). Ta chọn hệ trục tọa độ \(Oxy\) có gốc là trung điểm của đoạn thẳng \({F_1}{F_2}\). Trục \(Oy\) là đường trung trực của \({F_1}{F_2}\) và \({F_2}\) nằm trên tia \(Ox\) (Hình 8). Khi đó \({F_1}( - c;0),{F_2}(c;0)\) là các tiêu diểm của elip (E) Giả sử điểm \(M\left( {x;y} \right)\) thuộc elip (E) Chứng minh rằng: a) \(M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}\) b) \(M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}\) c) \(M{F_1}^2 - M{F_2}^2 = 4cx\) Lời giải chi tiết: a) Ta có: \(\overrightarrow {M{F_1}} = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}\) b) Ta có: \(\overrightarrow {M{F_2}} = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}\) c) \(M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx\) HĐ 6 Sử dụng đẳng thức c) ở trên và đẳng thức \(M{F_1} + M{F_2} = 2a\), chứng minh: a) \(M{F_1} - M{F_2} = \frac{{2c}}{a}x\) b) \(M{F_1} = a + \frac{c}{a}x\) c) \(M{F_2} = a - \frac{c}{a}x\) Lời giải chi tiết: a) Ta có: \(M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).2a = 4cx\) \( \Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{a}x\) b) Ta có: \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = 2a\left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{a}x\left( 2 \right)\end{array} \right.\) Cộng hai vế của (1) và (2) ta được: \(2M{F_1} = 2a + \frac{{2c}}{a}x \Rightarrow M{F_1} = a + \frac{c}{a}x\) c) Ta có: \(M{F_2} = 2a - M{F_1} = 2a - \left( {a + \frac{c}{a}x} \right) = a - \frac{c}{a}x\) VD 4 Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Giả sử M là điểm thuộc elip và có hoành độ là 2. Tìm độ dài của các bán kính qua tiêu của điểm M. Phương pháp giải: Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) + Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\) Lời giải chi tiết: Ta có \(c = \sqrt {{a^2} - {b^2}} = \sqrt {25 - 9} = 4\). Do đó \(e = \frac{c}{a} = \frac{4}{5} = 0,8\). Vậy độ dài các bán kính qua tiêu của điểm M là: \(M{F_1} = a + \frac{c}{a}x = 5 + 0,8.2 = 6,6;M{F_2} = a - \frac{c}{a}x = 5 - 0,8.2 = 3,4\) VD 5 Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\). Giả sử \(M\left( {x;y} \right)\) là điểm thuộc elip. Tìm giá trị lớn nhất và bé nhất của bán kính qua tiêu \(M{F_1}\) và \(M{F_2}\) Phương pháp giải: Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) + Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\) \(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\) \(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\) Lời giải chi tiết: Vì \( - a \le x \le a\) nên \(a + \frac{c}{a}\left( { - a} \right) \le a + \frac{c}{a}x \le a + \frac{c}{a}\left( a \right) \Leftrightarrow a - c \le M{F_1} \le a + c\) Vậy \(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\) Tương tự với \(M{F_2}\), ta có \( - a \le x \le a \Rightarrow a \ge - x \ge - a\) hay \( - a \le x \le a\) nên \(a - \frac{c}{a}\left( a \right) \le a - \frac{c}{a}x \le a - \frac{c}{a}\left( { - a} \right) \Leftrightarrow a - c \le M{F_2} \le a + c\) Vậy \(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\) Bài 3 Cho elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) với tiêu điểm \({F_2}\left( {\sqrt 5 ;0} \right)\). Tìm tọa độ \(M \in \left( E \right)\) sao cho độ dài \({F_2}M\) nhỏ nhất Phương pháp giải: Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) + Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\) \(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\) \(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\) Lời giải chi tiết: Elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) có \(a = 3,b = 2 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt 5 \) Độ dài bán kính qua tiêu \(M{F_2} = a - \frac{c}{a}x = 3 - \frac{{\sqrt 5 }}{3}x.\) Vì \(M{F_2}\) có độ dài nhỏ nhất là \(a - c\) khi \(x = a\) nên \(M{F_2}\) có độ dài nhỏ nhất là \(3 - \sqrt 5 \) khi \(x = 3.\) Mà \(M \in (E)\) \( \Rightarrow \frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1 \Rightarrow {y^2} = 4\left( {1 - \frac{{{x^2}}}{9}} \right) = 4\left( {1 - \frac{{{3^2}}}{9}} \right) = 0\) Vậy \(M\left( {3;0} \right)\) thì \(M{F_2}\) có độ dài nhỏ nhất bằng \(3 - \sqrt 5 \).
|




















Danh sách bình luận