Giải mục 5 trang 45, 46 Chuyên đề học tập Toán 10 - Cánh diều

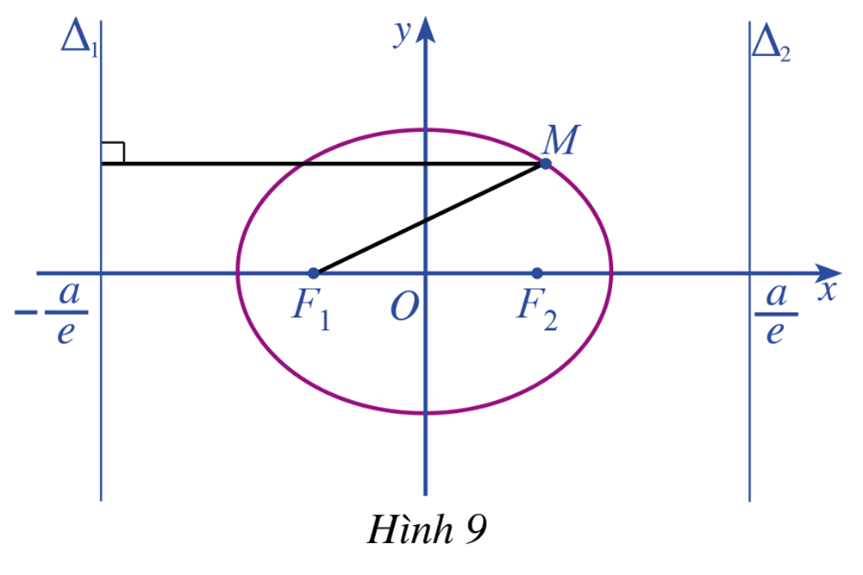
HĐ 7

Cho elip (E) \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)

Xét đường thẳng \({\Delta _1}:x =  - \frac{a}{e}\) với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\) (Hình 9), tính:

a) Khoảng cách \(d\left( {M,{\Delta _1}} \right)\) từ điểm \(M\left( {x;y} \right)\) đến đường thẳng \({\Delta _1}\)

b) Tỉ số \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}}\)

Lời giải chi tiết:

a) Viết lại phương trình đưởng thẳng \({\Delta _1}\) ở dạng: \(x + 0y + \frac{a}{e} = 0\)

Với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\), ta có: \(d\left( {M,{\Delta _1}} \right) = \frac{{\left| {x + 0y + \frac{a}{e}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \frac{{\left| {a + ex} \right|}}{e}\)

b) Do \(M{F_1} = a + ex > 0\) nên \(M{F_1} = \left| {a + ex} \right| \Rightarrow d\left( {M,{\Delta _1}} \right) = \frac{{M{F_1}}}{e}\)

Vậy \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = e\)

Luyện tập - vận dụng 4

Viết phương trình chính tắc của elip, biết tiêu điểm \({F_2}(5;0)\) và đường chuẩn ứng với tiêu điểm đó là \(x = \frac{{36}}{5}.\)

Phương pháp giải:

Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)

+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)

+ Ứng với tiêu điểm \({F_1}( - c;0)\), có đường chuẩn \({\Delta _1}:x + \frac{a}{e} = 0\)

+ Ứng với tiêu điểm \({F_2}(5;0)\), có đường chuẩn \({\Delta _2}:x - \frac{a}{e} = 0\)

Lời giải chi tiết:

Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)

(E) có tiêu điểm \({F_2}(c;0) = (5;0) \Rightarrow c = 5\)

Ứng với tiêu điểm \({F_2}(3;0)\), có đường chuẩn \({\Delta _2}:x = \frac{a}{e} = \frac{{36}}{5}\)

Mà \(e = \frac{c}{a} = \frac{5}{a} \Rightarrow \frac{a}{e} = \frac{{{a^2}}}{5} = \frac{{36}}{5} \Leftrightarrow {a^2} = 36\) hay \(a = 6\). Suy ra \(b = \sqrt {{a^2} - {c^2}}  = \sqrt {{6^2} - {5^2}}  = \sqrt {11} \)

Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{11}} = 1\)