Giải mục 4 trang 10 SGK Toán 11 tập 2 - Cánh DiềuGiáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
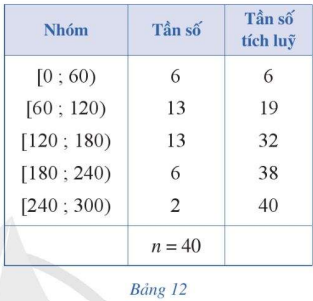
HĐ 6 Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm (đơn vị: phút) và lập bảng số ghép nhóm bao gồm cả tần số tích lũy như Bảng 12. a) Tìm trung vị \({M_e}\) của mẫu số liệu ghép nhóm đó. Trung vị \({M_e}\) còn gọi là tứ phân vị thứ hai \({Q_2}\) của mẫu số liệu trên. b) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{40}}{4} = 10\) có đúng không? Tìm đầu mút trái \(s\), độ dài \(h\), tần số \({n_2}\) của nhóm 2; tần số tích lũy \(c{f_1}\) của nhóm 1. Sau đó, hãy tính giá trị \({Q_1}\) theo công thức sau: \({Q_1} = s + \left( {\frac{{10 - c{f_1}}}{{{n_2}}}} \right).h\). Giá trị nói trên được gọi là tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đã cho. c) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\) có đúng không? Tìm đầu mút trái \(t\), độ dài \(l\), tần số \({n_3}\) của nhóm 3; tần số tích lũy \(c{f_2}\) của nhóm 2. Sau đó, hãy tính giá trị \({Q_3}\) theo công thức sau: \({Q_3} = t + \left( {\frac{{30 - c{f_2}}}{{{n_3}}}} \right).l\). Giá trị nói trên được gọi là tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu đã cho. Phương pháp giải: Áp dụng các công thức đã được học và công thức được cho để thực hiện bài toán. Lời giải chi tiết: a) \({M_e} = 120 + \left( {\frac{{20 - 19}}{{13}}} \right).60 = \frac{{1620}}{{13}}\) b) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10 - Đầu mút trái của nhóm 2: 60 - Độ dài của nhóm 2: 60 - Tần số của nhóm 2: 13 - Tần số tích lũy của nhóm 1: 6 \({Q_1} = 60 + \left( {\frac{{10 - 6}}{{13}}} \right).60 = \frac{{1020}}{{13}}\) c) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30 - Đầu mút trái của nhóm 3: 120 - Độ dài của nhóm 3: 60 - Tần số của nhóm 3: 13 - Tần số tích lũy của nhóm 2: 19 \({Q_3} = 120 + \left( {\frac{{20 - 19}}{{13}}} \right).60 = \frac{{1620}}{{13}}\) LT 6 Tìm tứ phân vị của mẫu số liệu trong Bảng 1. Phương pháp giải: Dựa vào kiến thức tứ phân vị vừa làm để xác định. Lời giải chi tiết:
Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60 + Đầu mút trái của nhóm 3: 8 + Độ dài của nhóm 3: 4 + Tần số của nhóm 3: 48 + Tần số tích lũy \(c{f_2}\) của nhóm 2: 42 \({M_e} = 8 + \left( {\frac{{60 - 42}}{{48}}} \right).4 = 9,5\) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30 + Đầu mút trái của nhóm 2: 4 + Độ dài của nhóm 2: 4 + Tần số của nhóm 2: 29 + Tần số tích lũy \(c{f_1}\) của nhóm 1 là: 13 \({Q_1} = 4 + \left( {\frac{{30 - 13}}{{29}}} \right).4 \approx 6,34\) Nhóm 3 là nhóm đầu tiên có tần số lớn hơn hoặc bằng 90 + Đầu mút trái của nhóm 3: 8 + Độ dài của nhóm 3: 4 + Tần số của nhóm 3: 48 + Tần số tích lũy \(c{f_2}\) của nhóm 2: 42 \({M_e} = 8 + \left( {\frac{{90 - 42}}{{48}}} \right).4 = 12\)
|





















Danh sách bình luận