Giải mục 3 trang 94, 95 SGK Toán 11 tập 1 - Chân trời sáng tạo

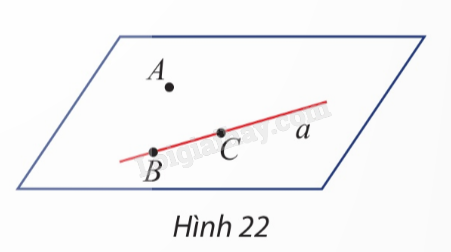
Hoạt động 8

Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.

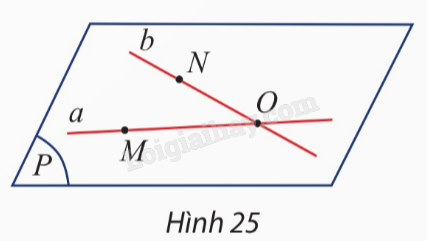
Phương pháp giải:

Áp dụng các tính chất:

‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Lời giải chi tiết:

Áp dụng tính chất 2, ta có duy nhất một mặt phẳng đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(\left( {ABC} \right)\).

Áp dụng tính chất 3, ta có đường thẳng \(a\) có hai điểm phân biệt \(B,C\) nằm trong mặt phẳng \(\left( {ABC} \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( {ABC} \right)\).

Hoạt động 9

Hai đường thẳng phân biệt \(a\) và \(b\) cắt nhau tại điểm \(O\). Trên \(a,b\) lấy lần lượt hai điểm \(M,N\) khác \(O\). Gọi \(\left( P \right)\) là mặt phẳng đi qua ba điểm \(M,N,O\) (Hình 25). Mặt phẳng \(\left( P \right)\) có chứa cả hai đường thẳng \(a\) và \(b\) không? Giải thích.

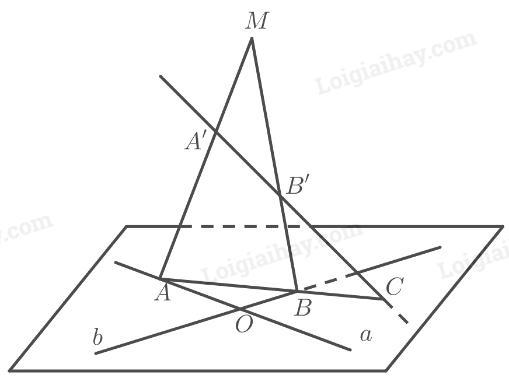
Phương pháp giải:

Áp dụng các tính chất:

‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Lời giải chi tiết:

Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).

Áp dụng tính chất 3, ta có

– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).

– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).

Thực hành 7

Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và điểm \(M\) không thuộc \(mp\left( {a,b} \right)\).

a) Tìm giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\).

b) Lấy \(A,B\) lần lượt là hai điểm trên \(a,b\) và khác với điểm \(O\). Tìm giao tuyến của \(\left( {MAB} \right)\) và \(mp\left( {a,b} \right)\).

c) Lấy điểm \(A'\) trên đoạn \(MA\) và điểm \(B'\) trên đoạn \(MB\) sao cho đường thẳng \(A'B'\) cắt \(mp\left( {a,b} \right)\) tại \(C\). Chứng minh ba điểm \(A,B,C\) thẳng hàng.

Phương pháp giải:

‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.

‒ Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.

Lời giải chi tiết:

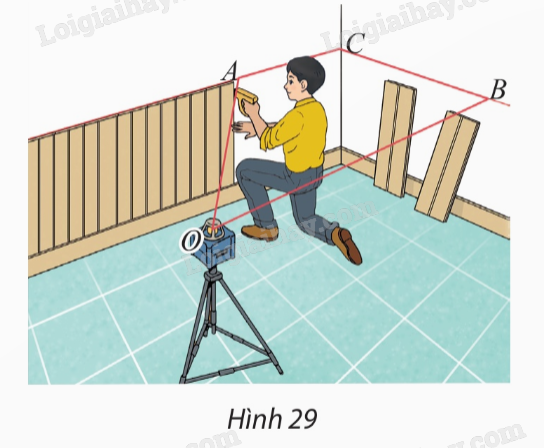
a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {M,a} \right)\\M \in \left( {M,b} \right)\end{array} \right\} \Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\\\left. \begin{array}{l}O \in a \subset \left( {M,a} \right)\\O \in b \subset \left( {M,b} \right)\end{array} \right\} \Rightarrow O \in \left( {M,a} \right) \cap \left( {M,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\) là đường thẳng \(MO\).

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {MAB} \right)\\A \in a \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow A \in \left( {MAB} \right) \cap \left( {a,b} \right)\\\left. \begin{array}{l}B \in \left( {MAB} \right)\\B \in b \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow B \in \left( {MAB} \right) \cap \left( {a,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) là đường thẳng \(AB\) (1).

c) Ta có:

\(\left. \begin{array}{l}A' \in MA \subset \left( {MAB} \right)\\B' \in MB \subset \left( {MAB} \right)\end{array} \right\} \Rightarrow A'B' \subset \left( {MAB} \right)\)

Vì \(C \in A'B' \subset \left( {MAB} \right)\) và \(C \in mp\left( {a,b} \right)\) nên điểm \(C\) nằm trên giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) (2).

Từ (1) và (2) suy ra ba điểm \(A,B,C\) thẳng hàng.

Vận dụng 2

Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.

Phương pháp giải:

Áp dụng các tính chất:

‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

‒ Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

Lời giải chi tiết:

‒ Với ghế 4 chân, nếu 4 điểm tại chân ghế không thuộc một mặt phẳng thì ghế có thể bị khập khiễng.

‒ Với ghế 3 chân, ta chỉ xác định được duy nhất một mặt phẳng đi qua 3 điểm thuộc chân ghế nên ghế ba chân không thể khập khiễng.

Vận dụng 4

Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường trong Hình 29.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

Từ Hình 29 ta thấy: Giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường là \(AC\) và \(BC\).