Bài 1 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạoCho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\). a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\). b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\). Quảng cáo
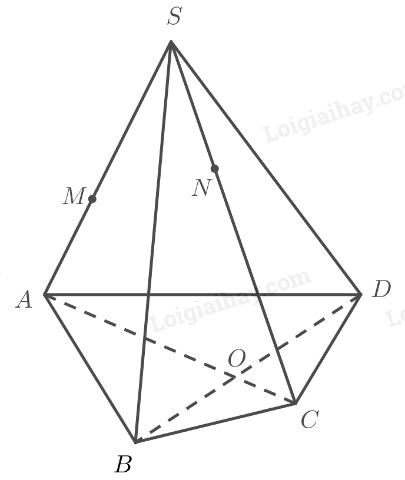
Đề bài Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\). a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\). b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\). Phương pháp giải - Xem chi tiết ‒ Để chứng minh đường thẳng nằm trong mặt phẳng, ta chứng minh đường thẳng đó có hai điểm phân biệt nằm trong mặt phẳng. ‒ Để chứng minh một điểm nằm trong mặt phẳng, ta chứng minh điểm đó nằm trên một đường thẳng nằm trong mặt phẳng. Lời giải chi tiết
a) Ta có: \(\left. \begin{array}{l}M \in SA \subset \left( {SAC} \right)\\N \in SC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow MN \subset \left( {SAC} \right)\) b) Ta có: \(\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
