Giải mục 3 trang 77, 78 SGK Toán 11 tập 2 - Chân trời sáng tạo

Hoạt động 3

Cho hai đường thẳng chéo nhau \(a\) và \(b\). Gọi \(\left( Q \right)\) là mặt phẳng chứa \(b\) và song song với \(a\). Gọi \(\left( P \right)\) là mặt phẳng chứa đường thẳng \(a\), vuông góc với \(\left( Q \right)\) và cắt \(b\) tại điểm \(J\). Trong \(\left( P \right)\), gọi \(c\) là đường thẳng đi qua \(J\), vuông góc với \(a\) và cắt \(a\) tại điểm \(I\).

Đường thẳng \(IJ\) có vuông góc với \(b\) không? Giải thích.

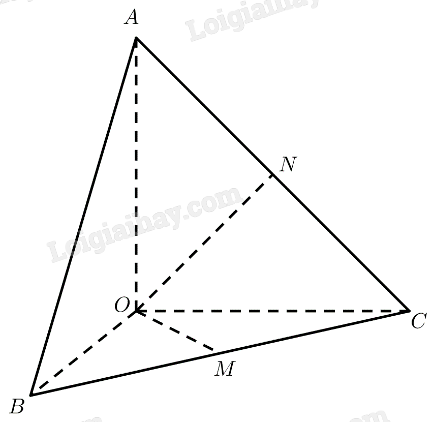
Phương pháp giải:

Chứng minh \(IJ\) vuông góc với mặt phẳng \(\left( Q \right)\) chứa đường thẳng \(b\).

Lời giải chi tiết:

Gọi \(\left( R \right)\) là mặt phẳng chứa \(a\)và song song với \(\left( Q \right)\). Ta có:

\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = a\end{array} \right\} \Rightarrow a\parallel a'\)

Mà \(IJ \bot a \Rightarrow IJ \bot a'\)

\(\left. \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = a'\\IJ \subset \left( P \right),IJ \bot a'\end{array} \right\} \Rightarrow IJ \bot \left( Q \right)\)

Mà \(b \subset \left( Q \right) \Rightarrow IJ \bot b\).

Thực hành 3

Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đều bằng \(a\) và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:

a) \(OA\) và \(BC\);

b) \(OB\) và \(AC\).

Phương pháp giải:

Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

Lời giải chi tiết:

a) Gọi \(M\) là trung điểm của \(BC\).

Tam giác \(OBC\) vuông cân tại \(O \Rightarrow OM \bot BC\)

\(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot OM\)

\( \Rightarrow d\left( {OA,BC} \right) = OM = \frac{1}{2}BC = \frac{1}{2}\sqrt {O{B^2} + O{C^2}}  = \frac{{a\sqrt 2 }}{2}\)

b) Gọi \(N\) là trung điểm của \(AC\).

Tam giác \(OAC\) vuông cân tại \(O \Rightarrow ON \bot AC\)

\(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right) \Rightarrow OB \bot ON\)

\( \Rightarrow d\left( {OB,AC} \right) = ON = \frac{1}{2}AC = \frac{1}{2}\sqrt {O{A^2} + O{C^2}}  = \frac{{a\sqrt 2 }}{2}\)

Vận dụng 2

Một căn phòng có trần cao 3,2 m. Tỉnh khoảng cách giữa một đường thẳng \(a\) trên trần nhà và đường thẳng \(b\) trên sàn nhà.

Phương pháp giải:

Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

Lời giải chi tiết:

Vì trần nhà và sàn nhà song song với nhau nên đường thẳng \(a\) nằm trên trần nhà song song với sàn nhà.

Vậy khoảng cách giữa đường thẳng \(a\) trên trần nhà và đường thẳng \(b\) trên sàn nhà bằng khoảng cách giữa trần nhà và sàn nhà. Khoảng cách đó bằng 3,2 m.