Bài 4 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo

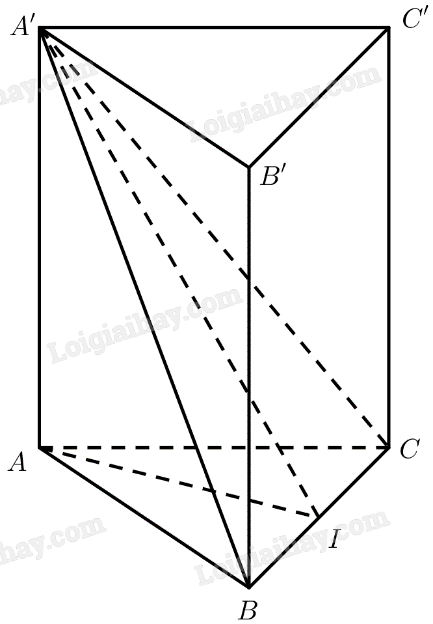
Đề bài

Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB = a$, góc giữa hai mặt phẳng $\left( {A'BC} \right)$ và $\left( {ABC} \right)$ bằng ${60^ \circ }$.

a) Tính khoảng cách giữa hai đáy của hình lăng trụ.

b) Tinh thể tích của khối lăng trụ.

Lời giải chi tiết

 

a) Gọi $I$ là trung điểm của $BC$.

Tam giác $ABC$ đều $\Rightarrow AI \bot BC$

Tam giác $A'BC$ cân tại $A' \Rightarrow A'I \bot BC$

$\Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }$

Tam giác $ABC$ đều $\Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}$

$\Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}$

b) ${S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}$

${V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}$