Giải mục 2 trang 85, 86, 87 SGK Toán 8 tập 2 - Kết nối tri thứcCho hai tam giác ABC và A'B'C' có độ dài các cạnh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
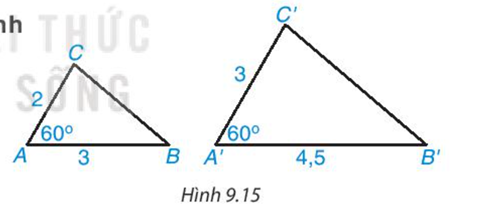
HĐ2 Video hướng dẫn giải Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng \(\widehat A = \widehat {A'} = 60^0\)
- So sánh các tỉ số \(\frac{{A'B'}}{{AB}}{;^{}}\frac{{A'C'}}{{AC}}\) - Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số \( \frac {B′C′} {BC} \) - Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu? Phương pháp giải: Quan sát hình 9.15 để tính tỉ số các đoạn thẳng Lời giải chi tiết: - Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{3}{2}\) - Có \(\frac{{B'C'}}{{BC}} = \frac{3}{2}\) - Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{3}{2}\) CH Video hướng dẫn giải Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
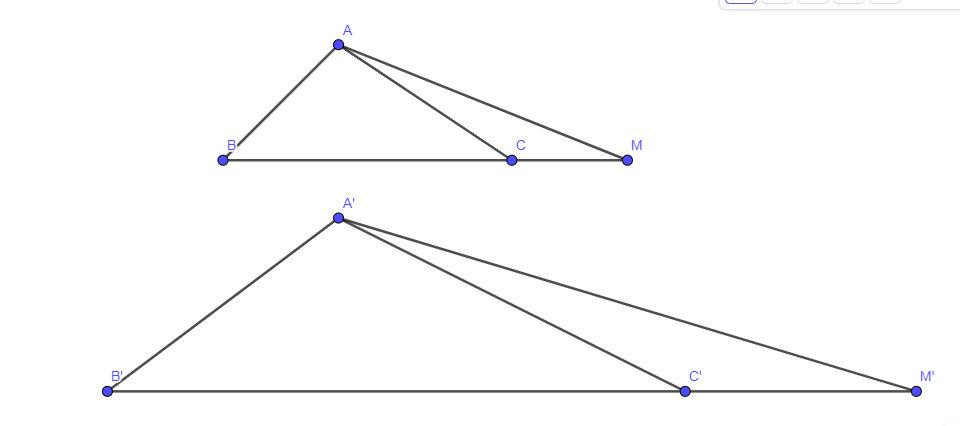
Phương pháp giải: Qua sát hình 9. 17 và định lí trường hợp đồng dạng cạnh – góc – cạnh để tìm các cặp tam giác đồng dạng. Lời giải chi tiết: Các cặp tam giác đồng dạng: \(\Delta ACB \backsim \Delta MPN\) LT2 Video hướng dẫn giải Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho \(\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\). Chứng minh rằng ΔA'B'M' ∽ ΔABM
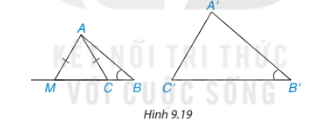
Phương pháp giải: Áp đụng định lí trường hợp đồng dạng canh – góc – cạnh để chứng minh \(\Delta A'B'M' \backsim \Delta ABM\) Lời giải chi tiết: Ta có: \(\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\\ \Rightarrow \frac{{MB - BC}}{{MB}} = \frac{{M'B' - B'C'}}{{M'B'}}\\ \Rightarrow 1 - \frac{{BC}}{{MB}} = 1 - \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{M'B'}}{{MB}} = \frac{{B'C'}}{{BC}}(1)\end{array}\) Vì ΔA'B'C' ∽ ΔABC suy ra: \(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}(2)\end{array}\) Từ (1) và (2) suy ra: \(\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\) Xét tam giác ABM và tam giác A”B”M’ có: \(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\end{array}\) Suy ra \(\Delta A'B'M' \backsim \Delta ABM\) TL Video hướng dẫn giải Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {B'} = \widehat B\) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao? Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho \( \Delta AMC \) cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'. Phương pháp giải: Áp dụng định lí trường hợp đồng dạng cạnh - góc – cạnh Lời giải chi tiết: Khi góc ACB là góc tù, lấy điểm M trên tia BC sao cho tam giác AMC cân tại A nên AM = AC
Khi đó \(\Delta A'B'C' \backsim \Delta ABM\) Như vậy nhận xét của Lan không chính xác.
|





















Danh sách bình luận