Giải bài 9.7 trang 90 SGK Toán 8 tập 2 - Kết nối tri thứcCho AM, BN, CP là các đường trung tuyến của tam giác ABC Quảng cáo
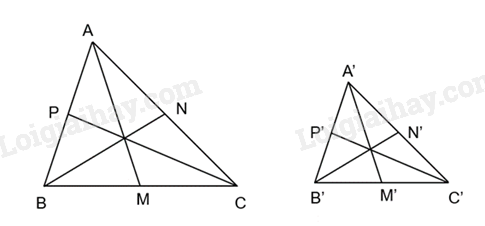
Đề bài Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC Chứng minh rằng \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}} = \frac{{C'P'}}{{CP}}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để chứng minh. Lời giải chi tiết
Vì ΔA’B’C’ ∽ ΔABC => ΔA’M’B’ ∽ ΔAMB => \(\frac{{A'M'}}{{AM}} = \frac{{A'B'}}{{AB}}(1)\) (1) Vì \(\Delta A'B'C'\) ∽ ΔABC => Vì ΔA′B′N′ ∽ ΔABN => \(\frac{{B'N'}}{{BN}} = \frac{{A'B'}}{{AB}}\) (2) Từ (1) và (2) => \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}}\)(3) Vì ΔA’B’C’ ∽ ΔABC => Vì ΔA’C’P’ ∽ ΔACP => \(\frac{{C'P'}}{{CP}} = \frac{{A'C'}}{{AC}}\) (4) Vì ΔA′B′C′ ∽ ΔABC => ΔA′M′C′ ∽ ΔAMC => \(\frac{{A'M'}}{{AM}} = \frac{{A'C'}}{{AC}}\) (5) Từ (4) và (5) => \(\frac{{C'P'}}{{CP}} = \frac{{A'M'}}{{AM}}\) (6) Từ (3) và (6) => \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}} = \frac{{C'P'}}{{CP}}\)
|




















Danh sách bình luận