Giải mục 2 trang 61, 62, 63, 64 Chuyên đề học tập Toán 10 - Chân trời sáng tạoCho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
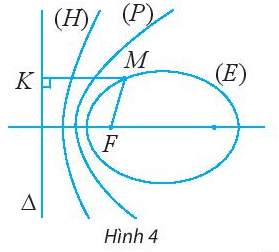
HĐ2 Cho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Tìm mối liên hệ giữa tỉ số \(\frac{{MF}}{{d(M,\Delta )}}\) và tên gọi của đường conic đó.
Lời giải chi tiết: + Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (E)\) \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{a + ex}}{{\frac{{a + ex}}{e}}} = e\), \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{a - ex}}{{\frac{{a - ex}}{e}}} = e\) Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} < 1\) + Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (H)\) \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a + ex} \right|}}{{\left| {x + \frac{a}{e}} \right|}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\); \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a - ex} \right|}}{{\left| {x - \frac{a}{e}} \right|}} = \frac{{\left| {a - ex} \right|}}{{\frac{{\left| {a - ex} \right|}}{e}}} = e\) ; Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} > 1\) + Parabol (P) \({y^2} = 2px\) \(\frac{{MF}}{{d(M,\Delta )}} = e = 1\) Kết luận các đường conic đều có \(\frac{{MF}}{{d(M,\Delta )}} = e\) và \(\frac{{MF}}{{d(M,\Delta )}} < 1\) thì conic là đường elip \(\frac{{MF}}{{d(M,\Delta )}} = 1\) thì conic là đường parabol \(\frac{{MF}}{{d(M,\Delta )}} > 1\) thì conic là đường hypebol
Thực hành 2 Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau: a) \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\) b) \(\frac{{{x^2}}}{{12}} - \frac{{{y^2}}}{4} = 1\) c) \({y^2} = \frac{1}{2}x\) Phương pháp giải: a) Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} - {b^2}} \) + Tâm sai của elip: \(e = \frac{c}{a}\) + Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) + Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\). b) Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} + {b^2}} \) + Tâm sai của hypebol: \(e = \frac{c}{a}\) + Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) + Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\). c) Parabol (P) \({y^2} = 2px\) + Tâm sai \(e = 1\) + Tiêu điểm \(F(\frac{p}{2};0)\) + Đường chuẩn: \(\Delta :x = - \frac{p}{2}\) Lời giải chi tiết: a) Elip (E): \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\), suy ra \(c = \sqrt {{a^2} - {b^2}} = \sqrt 3 \) + Tâm sai của elip: \(e = \frac{c}{a} = \frac{{\sqrt 3 }}{{\sqrt 5 }} = \frac{{\sqrt {15} }}{5}\) + Tiêu điểm \({F_1}( - \sqrt 3 ;0),{F_2}(\sqrt 3 ;0)\) + Đường chuẩn: \({\Delta _1}:x = - \frac{{5\sqrt 3 }}{3}\) và \({\Delta _2}:x = \frac{{5\sqrt 3 }}{3}\). b) Hypebol (H): \(\frac{{{x^2}}}{{12}} - \frac{{{y^2}}}{4} = 1\), \(c = \sqrt {{a^2} + {b^2}} = 4\) + Tâm sai của hypebol: \(e = \frac{c}{a} = \frac{4}{{2\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\) + Tiêu điểm \({F_1}( - 4;0),{F_2}(4;0)\) + Đường chuẩn: \({\Delta _1}:x = - 3\) và \({\Delta _2}:x = 3\). c) Parabol (P): \({y^2} = \frac{1}{2}x\), suy ra \(p = \frac{1}{4}\) + Tâm sai \(e = 1\) + Tiêu điểm \(F(\frac{1}{8};0)\) + Đường chuẩn: \(\Delta :x = - \frac{1}{8}\)
Vận dụng 2 Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol.
(Nguồn: https://vi.wikipedia.org/wiki/oumuamud) Phương pháp giải: Đường conic có tâm sai e: + \(0 < e < 1\) thì conic là đường elip + \(e = 1\) thì conic là đường parabol + \(e > 1\) thì conic là đường hypebol Lời giải chi tiết:
|




















Danh sách bình luận