Giải mục 2 trang 41 Chuyên đề học tập Toán 10 - Cánh diều

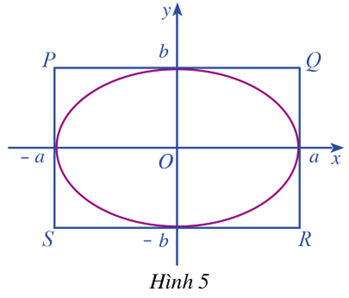
HĐ 3

a) Nêu nhận xét về vị trí bốn đỉnh của elip \(\left( E \right)\) với bốn cạnh của hình chữ nhật cơ sở.

b) Cho điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\). Tìm giá trị nhỏ nhất và lớn nhất của x và của y.

Lời giải chi tiết:

a) Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có:

+ Hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)

+ Bốn đỉnh của elip là trung điểm của các cạnh của hình chữ nhật cơ sở

b) Nếu điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

\( \Rightarrow \frac{{{x^2}}}{{{a^2}}} \le 1,\frac{{{y^2}}}{{{b^2}}} \le 1 \Leftrightarrow {x^2} \le {a^2},{y^2} \le {b^2}\)

\( \Leftrightarrow  - a \le x \le a, - b \le y \le b\).

Dó đó mọi điểm của elip nếu không phải đỉnh thì đều nằm trong hình chữ nhật

Khi đó Giá trị lớn nhất và nhỏ nhất của x là a và -a, Giá trị lớn nhất và nhỏ nhất của y là b và -b

Luyện tập - vận dụng 1

Viết phương trình chính tắc của elip, biết \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của nó

Phương pháp giải:

Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) . Khi đó ta có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)

Lời giải chi tiết:

Ta có \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của elip, suy ra \(a = 4,b = 2\).

Khi đó phương trình chính tắc của elip là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\)

HĐ 4

Quan sát elip \(\left( E \right)\) phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > b > 0\) và hình chữ nhật cơ sở PQRS của \(\left( E \right)\)(Hình 5)

a) Tính tỉ số giữa hai cạnh \(\frac{{QR}}{{PQ}}\) của hình chữ nhật \(PQRS\)

b) Tỉ số \(\frac{{QR}}{{PQ}}\) phản ánh đặc điểm gì của \(\left( E \right)\) về hình dạng?

Phương pháp giải:

Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)

Lời giải chi tiết:

a) Ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)

Suy ra \(QR = 2b,PQ = 2a \Rightarrow \frac{{QR}}{{PQ}} = \frac{{2b}}{{2a}} = \frac{b}{a}\)

b) Ta có \(\frac{{QR}}{{PQ}} = \frac{b}{a}\), vì \(0 < b < a\) nên \(0 < \frac{b}{a} < 1\). Tỉ số \(\frac{b}{a}\) phản ánh cụ thể hình dạng của \(\left( E \right)\) như sau:

+ Nếu tỉ số \(\frac{b}{a}\) càng bé thì hình chữ nhật cơ sở càng “dẹt”, do đó \(\left( E \right)\) càng “gầy”

+ Nếu tỉ số \(\frac{b}{a}\) càng lớn thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó \(\left( E \right)\) càng “béo”