Giải mục 2 trang 106 SGK Toán 8 tập 1 - Cánh diều

HĐ2

Cho hình bình hành ABCD (Hình 37).

a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.

b) So sánh các cặp góc: \(\widehat {DAB}\) và \(\widehat {BCD}\); \(\widehat {ABC}\) và \(\widehat {CDA}\).

c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.

Phương pháp giải:

Sử dụng chứng minh các tam giác tương ứng bằng nhau.

Lời giải chi tiết:

a) Xét tam giác ABD và tam giác CDB có:

\(\widehat {ABD} = \widehat {CDB}\) ( vì AB //CD)

BD chung

\(\widehat {ADB} = \widehat {CBD}\) (vì AD // BC)

Suy ra: \(\Delta ABD = \Delta CDB\)(g - c - g)

Suy ra: AB = CD, DA = BC.

b) Vì \(\Delta AB{\rm{D}} = \Delta C{\rm{D}}B\) (g - c - g) suy ra: \(\widehat {DAB}\) = \(\widehat {BCD}\)

Xét tam giác ABC và tam giác CDA có:

AB = CD (cmt)

Cạnh AC chung

BC = AD (cmt)

\(\Delta ABC = \Delta CDA (c - c - c) \Rightarrow \widehat {ABC} = \widehat {CDA}\) (2 góc tương ứng)

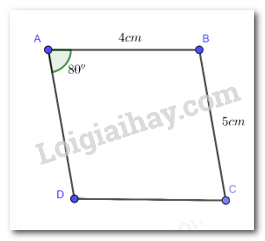
c) Xét tam giác OAB và OCD có:

\(\begin{array}{l}\widehat {OAB} = \widehat {OCD} (cmt)\\AB = CD (cmt)\\\widehat {OBA} = \widehat {ODC} (cmt)\end{array}\)

Suy ra: \(\Delta OAB = \Delta OC{\rm{D}}\) (g - c - g) suy ra: OA = OC; OB = OD (các cạnh tương ứng)

LT1

Cho hình bình hành ABCD có \(\widehat A = {80^o};AB = 4cm;BC = 5cm\). Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.

Phương pháp giải:

Vận dụng tính chất của hình bình hành.

Lời giải chi tiết:

Do ABCD là hình bình hành

Suy ra: CD = AB = 4cm

AD = BC = 5 cm

\(\widehat C = \widehat A = {80^o}\)

Nên: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\)