Giải bài 1 trang 107 SGK Toán 8 tập 1 - Cánh diềuCho tứ giác ABCD có Quảng cáo
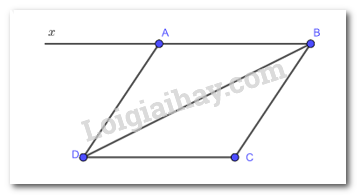
Đề bài Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {ABC} = \widehat {C{\rm{D}}A}\). Kẻ tia Ax là tia đối của tia AB. Chứng minh: a) \(\widehat {ABC} + \widehat {DAB} = {180^o}\) b) \(\widehat {xA{\rm{D}}} = \widehat {ABC};AD//BC\) c) Tứ giác ABCD là hình bình hành. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng các góc của 1 tứ giác bằng \({360^0}.\) Lời giải chi tiết
a, Tứ giác ABCD có: \(\widehat {ABC} + \widehat {BCD} + \widehat {CDA} + \widehat {DAB} = {360^0}\) \(\widehat {ABC} + \widehat {DAB} + \widehat {ABC} + \widehat {DAB} = {360^0}\)(do \(\widehat {DAB} = \widehat {BCD};\widehat {ABC} = \widehat {CDA}\)) \(\begin{array}{l}2\widehat {ABC} + 2\widehat {DAB} = {360^0}\\\widehat {ABC} + \widehat {DAB} = \dfrac{{{{360}^0}}}{2} = {180^0}\end{array}\) b, Ta có: \(\widehat {xAD} + \widehat {DAB} = {180^0}\)(do tia Ax là tia đối của tia AB) Nên \(\widehat {xAD} + \widehat {DAB} = \widehat {ABC} + \widehat {DAB}\) Suy ra \( \widehat {xAD} = \widehat {ABC}\) Suy ra AD//BC (hai góc đồng vị bằng nhau) c, Vì AD//BC nên \(\widehat {ADB} = \widehat {DBC}\) (2 góc so le trong) Xét \(\Delta ADB\) có \(\widehat {ABD} = {180^0} - \widehat {ADB} - \widehat {DAB} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 1 \right)\) (vì \(\widehat {ADB} = \widehat {DBC};\widehat {DAB} = \widehat {BCD})\) Xét \(\Delta CDB\) có: \(\widehat {BDC} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 2 \right)\) Từ (1), (2) suy ra \(\widehat {ABD} =\widehat {BDC}\) Xét \(\Delta ADB\) và \(\Delta BCD\) có: \(\left. \begin{array}{l}DB \; chung\\\widehat {ABD} = \widehat {BDC}\\\widehat {BAD} = \widehat {DBC}\end{array} \right\}\) Suy ra \(\Delta A{\rm{D}}B = \Delta C{\rm{D}}B\) Do đó \(A{\rm{D}} = BC,AB = CB\) Suy ra tứ giác ABCD có cặp cạnh đối bằng nhau nên ABCD là hình bình hành.
|




















Danh sách bình luận