Giải mục 1 trang 75, 76, 77 SGK Toán 9 tập 2 - Chân trời sáng tạo

HĐ1

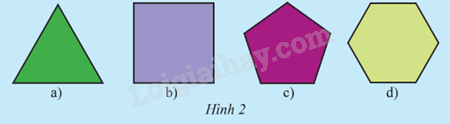
Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Chân trời sáng tạo

Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?

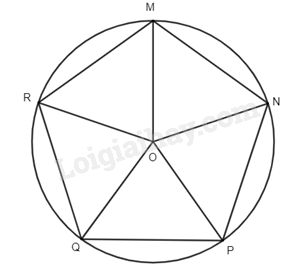
Phương pháp giải:

Nhìn hình nhận xét.

Lời giải chi tiết:

- Độ dài các cạnh của mỗi đa giác là bằng nhau.

- Số đo góc của mỗi đa giác là bằng nhau.

TH1

Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 9 Chân trời sáng tạo

Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung $\overset\frown{MN},\overset\frown{NP},\overset\frown{PQ},\overset\frown{QR},\overset\frown{RM}$ bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?

Phương pháp giải:

-  Đọc kĩ dữ kiện đề bài để vẽ hình

-  Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

Lời giải chi tiết:

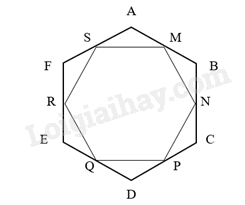
Các cung $\overset\frown{MN}, \overset\frown{NP}, \overset\frown{PQ}, \overset\frown{QR}, \overset\frown{RM}$ chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360^o : 5 = 72^o.

Ta có $\widehat {MON}$ là góc nội tiếp chắn cung MN suy ra $\widehat {MON}$ = 72^o .

Xét $\Delta$MON, có: OM = ON = R suy ra $\Delta$ MON cân tại O.

Suy ra $\widehat {OMN} = \widehat {ONM}$ (tính chất tam giác cân)

Suy ra $\widehat {OMN} = \widehat {ONM} = \frac{{{{180}^o} - \widehat {MON}}}{2} = {54^o}$.

Tương tự, ta có $\widehat {OPN} = \widehat {ONP} = {54^o}$.

Suy ra $\widehat {MPN} = \widehat {ONM} + \widehat {ONP} = {54^o} + {54^o} = {108^o}$.

Xét $\Delta$ OMN và $\Delta$ ONP có:

 $\widehat {MON} = \widehat {NOP}$;

 OM = OP;

 ON chung.

Suy ra  $\Delta$ OMN = $\Delta$ ONP (c – g – c).

Do đó, MN = NP (hai cạnh tương ứng).

Chứng minh tương tự ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau ( = 108^o).

Vậy MNPQR là một đa giác đều.

VD1

Trả lời câu hỏi Vận dụng 1 trang 77 SGK Toán 9 Chân trời sáng tạo

Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?

Phương pháp giải:

-  Đọc kĩ dữ kiện đề bài để vẽ hình

-  Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

Lời giải chi tiết:

Do ABCDEF là lục giác đều nên:

$\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = \widehat F = {120^o}$.

- AB = BC = CD = DE = EF = FA.

Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.

Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.

Xét $\Delta$ SAM và $\Delta$ MBN có:

$\widehat A = \widehat B$ (chứng minh trên);

 AM = BN (chứng minh trên);

 SA = MB (chứng minh trên).

Suy ra $\Delta$ SAM = $\Delta$ MBN  (c – g – c).

Do đó, SM = MN (hai cạnh tương ứng).

Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM (1).

Vì AS = AM (chứng minh trên) suy ra $\Delta$ ASM cân tại A.

suy ra $\widehat {ASM} = \widehat {AMS}$ (tính chất tam giác cân)

Nên $\widehat {ASM} = \widehat {AMS} = \frac{{{{180}^o} - \widehat A}}{2} = {30^o}$ (tổng 3 góc trong của tam giác).

Tương tự ta thu được:

$\widehat {BMN} = \widehat {BNM} = \frac{{{{180}^o} - \widehat B}}{2} = 30$;

$\widehat {CNP} = \widehat {CPN} = \frac{{{{180}^o} - \widehat C}}{2} = {30^o}$;

$\widehat {DPQ} = \widehat {DQP} = \frac{{{{180}^o} - \widehat D}}{2} = {30^o}$;

$\widehat {EQR} = \widehat {ERQ} = \frac{{{{180}^o} - \widehat E}}{2} = {30^o}$;.

$\widehat {FRS} = \widehat {FSR} = \frac{{{{180}^o} - \widehat F}}{2} = {30^o}$

Ta có: 

$\widehat {RSM} = {180^o} - \widehat {FRS} - \widehat {ASM} = {180^o} - {30^o} - {30^o} = {120^o}$

Tương tự, ta được: 

$\widehat {AMN} = \widehat {MNP} = \widehat {NQP} = \widehat {PQR} = \widehat {QRS} = {120^o}$.   (2)

Từ (1) và (2), suy ra MNPQRS là đa giác đều.