Giải mục 1 trang 73, 74, 75 SGK Toán 11 tập 1 - Cánh Diều

HĐ 1

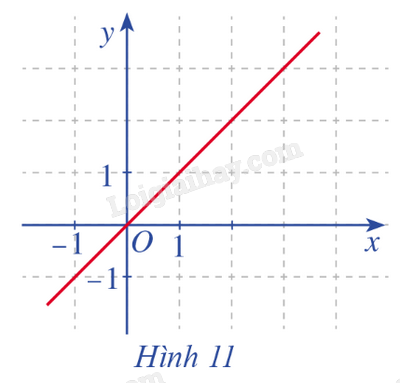
Quan sát đồ thị hàm số \(f\left( x \right) = x\) ở Hình 11.

a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\)

b) So sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) với \(f\left( 1 \right).\)

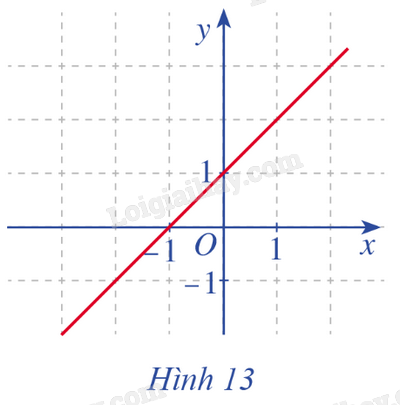
Phương pháp giải:

Sử dụng \(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)

Lời giải chi tiết:

a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} x = 1\)

b) \(f\left( 1 \right) = 1 \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right).\)

LT - VD 1

Xét tính liên tục của hàm số \(f\left( x \right) = {x^3} + 1\) tại \({x_0} = 1.\)

Phương pháp giải:

Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải chi tiết:

Ta có \(f\left( {{x_0}} \right) = f\left( 1 \right) = {1^3} + 1 = 2;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^3} + 1 = 1 + 1 = 2\)

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\)

Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0} = 1.\)

HĐ 2

Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)

a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?

b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.

Phương pháp giải:

Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải chi tiết:

a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)

\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)

b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)

LT - VD 2

Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 1,\,\,x < 2\\ - x,\,\,x \ge 2\end{array} \right.\) có liên tục trên \(\mathbb{R}\) hay không?

Phương pháp giải:

- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

- \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L\)

Lời giải chi tiết:

+) Với mỗi \({x_0} \in \left( { - \infty ;2} \right)\) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x - 1} \right) = {x_0} - 1 = f\left( {{x_0}} \right)\)

Do đó hàm số \(f\left( x \right)\) liên tục tại \({x_0} \in \left( { - \infty ;2} \right).\)

+) Với mỗi \({x_0} \in \left( {2; + \infty } \right)\) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x} \right) =  - {x_0} = f\left( {{x_0}} \right)\)

Do đó hàm số \(f\left( x \right)\) liên tục tại \({x_0} \in \left( {2; + \infty } \right).\)

+) Với mỗi \({x_0} = 2\) có \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x - 1} \right) = 2 - 1 = 1;\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - x} \right) =  - 2\)

\( \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\) do đó không tồn tại \(\mathop {\lim }\limits_{x \to 2} f\left( x \right).\)

Vậy hàm số \(f\left( x \right)\) gián đoạn tại \({x_0} = 2\) nên hàm số \(f\left( x \right)\) không liên tục trên \(\mathbb{R}.\)