Giải mục 1 trang 72, 73 SGK Toán 12 tập 2 - Cùng khám phá

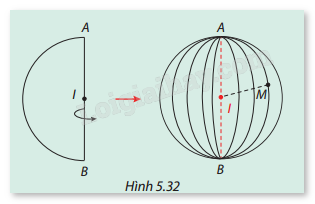
HĐ1

Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 12 Cùng khám phá

Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.

Phương pháp giải:

Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.

Lời giải chi tiết:

Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.

Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.

LT1

Trả lời câu hỏi Luyện tập 1 trang 73 SGK Toán 12 Cùng khám phá

Trong không gian Oxyz, cho mặt cầu (S) đi qua gốc toạ độ O, bán kính r = 5. Tìm toạ độ tâm I của (S), biết điểm I thuộc đường thẳng

\(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 4 + 2t}\end{array}} \right.\quad (t \in \mathbb{R}).\)

Phương pháp giải:

Gọi \(I(a,b,c)\) là tọa độ của tâm mặt cầu \(S\).

Vì mặt cầu \(S\) đi qua gốc tọa độ \(O(0,0,0)\), nên \(IO = r = 5\).

Đặt \(I\) nằm trên đường thẳng \(d\) và tìm giá trị \(t\) sao cho khoảng cách \(IO = 5\).

Giải phương trình để tìm \(t\), từ đó xác định tọa độ của \(I\).

Lời giải chi tiết:

Giả sử \(I(a,b,c)\) có tọa độ: \(a = 3 - t, b = t, c = 4 + 2t.\)

 Do \(IO = 5\), ta có: \(IO = \sqrt {{a^2} + {b^2} + {c^2}}  = 5.\)

 Thay \(a = 3 - t\), \(b = t\), \(c = 4 + 2t\) vào phương trình:

\(\begin{array}{l}\sqrt {{{(3 - t)}^2} + {t^2} + {{(4 + 2t)}^2}}  = 5.\\ \Leftrightarrow 9 - 6t + {t^2} + {t^2} + 16 + 16t + 4{t^2} = 25\\ \Leftrightarrow 6{t^2} + 10t + 25 = 25\\ \Leftrightarrow 2t(3t + 5) = 0\\ \Leftrightarrow t = 0,\,\,\,t =  - \frac{5}{3}\end{array}\)

Vậy có hai toạ độ tâm I thoả mãn là \(I(3;0;4)\) hoặc \(I\left( {\frac{{14}}{3}; - \frac{5}{3};\frac{2}{3}} \right)\).