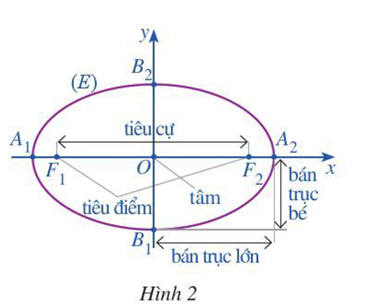
Giải mục 1 trang 39, 40 Chuyên đề học tập Toán 10 - Cánh diềuTrong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) (Hình 2) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
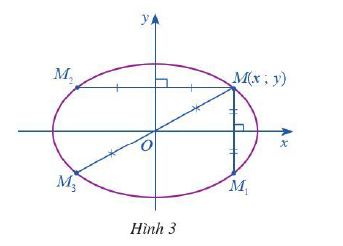
HĐ 1 Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) (Hình 2) a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của \(\left( E \right)\) b) \(\left( E \right)\) cắt trục \(Ox\) tịa các điểm \({A_1},{A_2}\) và cắt trục \(Oy\) tịa các điểm \({B_1},{B_2}\). Tìm độ dài các đoạn thẳng \(O{A_2},O{B_2}\) Phương pháp giải: Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) + 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\) Lời giải chi tiết: Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) có 4 đỉnh \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\) \( \Rightarrow O{A_2} = a;O{B_2} = b\) HĐ 2 Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) Cho điểm \(M\left( {x;y} \right)\) nẳm trên \(\left( E \right)\) (Hình 3) a) Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Tìm tọa độ của điểm \({M_1}\). Điểm \({M_1}\) có nằm trên \(\left( E \right)\) hay không? Tại sao? b) Gọi \({M_2}\) là điểm đối xứng của M qua trục Oy. Tìm tọa độ của điểm \({M_2}\). Điểm \({M_2}\) có nằm trên \(\left( E \right)\) hay không? Tại sao? c) Gọi \({M_3}\) là điểm đối xứng của M qua gốc O. Tìm tọa độ của điểm \({M_3}\). Điểm \({M_3}\) có nằm trên \(\left( E \right)\) hay không? Tại sao? Lời giải chi tiết: a) Điểm \({M_1}\) là điểm đối xứng của M qua trục Ox, nên \({M_1}\left( {x; - y} \right)\) \({M_1}\left( {x; - y} \right)\) thuộc Elip vì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) b) Điểm \({M_2}\) là điểm đối xứng của M qua trục Oy, nên \({M_2}\left( { - x;y} \right)\) \({M_2}\left( { - x;y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) c) Điểm \({M_3}\) là điểm đối xứng của M qua gốc O, nên \({M_3}\left( { - x; - y} \right)\) \({M_3}\left( { - x; - y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
|




















Danh sách bình luận