Giải mục 1 trang 26, 27, 28 SGK Toán 11 tập 2 - Chân trời sáng tạoSố lượng cá thể vi khuẩn của một mẻ nuôi cấy tuân theo công thức (Pleft( t right) = {50.10^{kt}}) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 1 Số lượng cá thể vi khuẩn của một mẻ nuôi cấy tuân theo công thức \(P\left( t \right) = {50.10^{kt}}\), trong đó \(t\) là thời gian tính bằng giờ kể từ thời điểm bắt đầu nuôi cấy, \(k\) là hằng số.
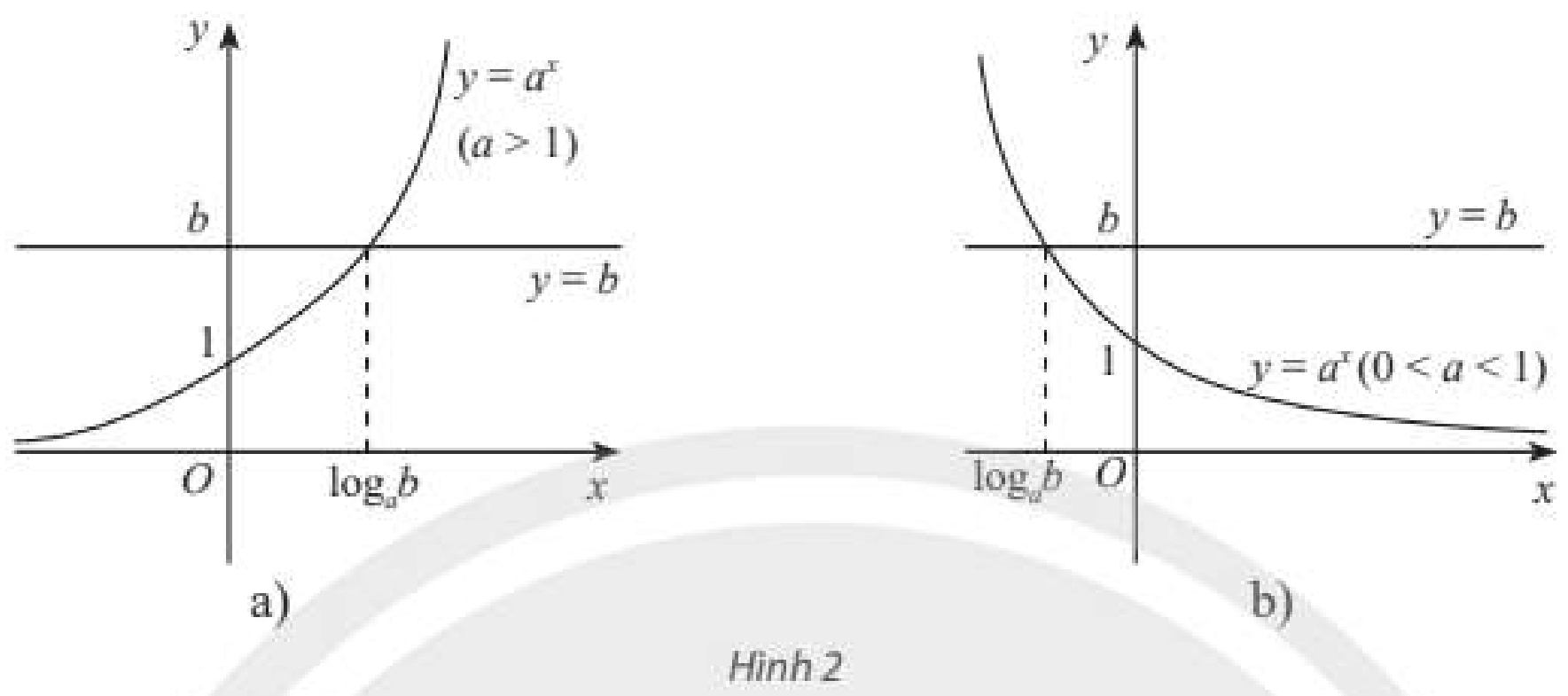
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101) a) Ban đầu mẻ có bao nhiêu cá thể vi khuẩn? b) Sau 1 giờ thì mẻ có 100 cá thể vi khuẩn. Tìm giá trị của \(k\) (làm tròn kết quả đến hàng phần mười). c) Sau bao lâu thì số lượng cá thể vi khuẩn đạt đến 50000? Phương pháp giải: a) Thay \(t = 0\) vào công thức \(P\left( t \right) = {50.10^{kt}}\). b) Thay \(t = 1,P\left( t \right) = 100\) vào công thức \(P\left( t \right) = {50.10^{kt}}\). c) Thay \(P\left( t \right) = 50000\) vào công thức \(P\left( t \right) = {50.10^{kt}}\). Lời giải chi tiết: a) Số cá thể vi khuẩn ban đầu mẻ có là: \(P\left( 0 \right) = {50.10^{k.0}} = {50.10^0} = 50\) (cá thể) b) Với \(t = 1,P\left( t \right) = 100\) ta có: \(P\left( 1 \right) = {50.10^{k.1}} \Leftrightarrow 100 = {50.10^k} \Leftrightarrow {10^k} = 2 \Leftrightarrow k = \log 2 \approx 0,3\) c) Thời gian để số lượng cá thể vi khuẩn đạt đến 50000 là: \(50000 = {50.10^{0,3t}} \Leftrightarrow {10^{0,3t}} = 1000 \Leftrightarrow 0,3t = \log 1000 \Leftrightarrow 0,3t = 3 \Leftrightarrow t = 10\) (giờ) Hoạt động 2 Cho đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) như Hình 2a (với \(a > 0\)) hay Hình 2b (với \(0 < a < 1\)). Từ đây, hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({a^x} = b\) trong hai trường hợp \(b > 0\) và \(b \le 0\).
Phương pháp giải: Quan sát đồ thị, dựa vào số điểm chung của đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\). Lời giải chi tiết: Khi \(b > 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) cắt nhau tại một điểm duy nhất. Khi đó phương trình \({a^x} = b\) có nghiệm duy nhất \(x = {\log _a}b\). Khi \(b \le 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) không có điểm chung. Khi đó phương trình \({a^x} = b\) vô nghiệm. Thực hành 1 Giải các phương trình sau: a) \({3^{x + 2}} = \sqrt[3]{9}\); b) \({2.10^{2{\rm{x}}}} = 30\); c) \({4^{2{\rm{x}}}} = {8^{2{\rm{x}} - 1}}\). Phương pháp giải: a) b) Đưa về phương trình \({a^x} = b\). c) Đưa 2 vế của phương trình về cùng cơ số. Lời giải chi tiết: a) \({3^{x + 2}} = \sqrt[3]{9} \Leftrightarrow {3^{x + 2}} = {9^{\frac{1}{3}}} \Leftrightarrow {3^{x + 2}} = {\left( {{3^2}} \right)^{\frac{1}{3}}} \Leftrightarrow {3^{x + 2}} = {3^{\frac{2}{3}}} \Leftrightarrow x + 2 = \frac{2}{3} \Leftrightarrow x = - \frac{4}{3}\) b) \({2.10^{2{\rm{x}}}} = 30 \Leftrightarrow {10^{2{\rm{x}}}} = 15 \Leftrightarrow 2{\rm{x}} = \log 15 \Leftrightarrow x = \frac{1}{2}\log 15\) c) \({4^{2{\rm{x}}}} = {8^{2{\rm{x}} - 1}} \Leftrightarrow {\left( {{2^2}} \right)^{2{\rm{x}}}} = {\left( {{2^3}} \right)^{2{\rm{x}} - 1}} \Leftrightarrow {2^{4{\rm{x}}}} = {2^{6{\rm{x}} - 3}} \Leftrightarrow 4{\rm{x}} = 6{\rm{x}} - 3 \Leftrightarrow - 2{\rm{x}} = - 3 \Leftrightarrow x = \frac{3}{2}\) Vận dụng 1 Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu \({M_0}\) là \(M\left( t \right) = {M_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\), trong đó \(t\) là thời gian tính từ thời điểm ban đầu và \(T\) là chu kì bán rã của chất. Đồng vị plutonium-234 có chu kì bản rã là 9 giờ. (Nguồn: https://pubchem.ncbi.nlm.nih.gov/element/Plutonium#section=Atomic- Mass-Half-Life-and-Decay) Từ khối lượng ban đầu 200 g, sau bao lâu thì sau bao lâu thì khối lượng plutonium-234 còn lại là: a) 100 g? b) 50 g? c) 20 g? Phương pháp giải: Thay \({M_0} = 200,T = 9\) và giá trị của \(M\left( t \right)\) vào công thức \(M\left( t \right) = {M_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\). Lời giải chi tiết: a) Với \({M_0} = 200,T = 9,M\left( t \right) = 100\) ta có: \(100 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{2} \Leftrightarrow \frac{t}{9} = 1 \Leftrightarrow t = 9\) Vậy sau 9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 100 g. b) Với \({M_0} = 200,T = 9,M\left( t \right) = 50\) ta có: \(50 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{4} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = {\left( {\frac{1}{2}} \right)^2} \Leftrightarrow \frac{t}{9} = 2 \Leftrightarrow t = 18\) Vậy sau 18 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g. c) Với \({M_0} = 200,T = 9,M\left( t \right) = 20\) ta có: \(20 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _{\frac{1}{2}}}\frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _2}10 \Leftrightarrow t = 9{\log _2}10 \approx 29,9\) Vậy sau 29,9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.
|




















Danh sách bình luận