Giải mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2 - Cùng khám pháTrong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số (y = x - 3), trục hoành và các đường thẳng (x = 1) và (x = 6). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
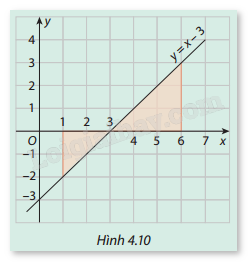
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 22 SGK Toán 12 Cùng khám phá Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = x - 3\), trục hoành và các đường thẳng \(x = 1\) và \(x = 6\).
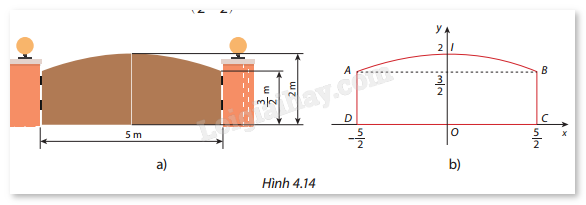
a) Tính diện tích của (H). b) Tính các tích phân \(\int_1^6 {(x - 3)} {\mkern 1mu} dx\) và \(\int_1^6 | x - 3|{\mkern 1mu} dx\). So sánh hai tích phân này với kết quả tính được ở câu a và rút ra nhận xét. Phương pháp giải: a) Diện tích (H) có thể tính bằng cách cộng diện tích của hai tam giác. Diện tích của tam giác được tính bằng công thức: \(S = \frac{1}{2} \times h \times \)đáy b) - Tính trực tiếp các tích phân \(\int_1^6 {(x - 3)dx} \) và \(\int_1^6 {\left| {x - 3} \right|dx} \). - So sánh kết quả của hai tích phân này với diện tích tính được ở câu a để rút ra nhận xét. Lời giải chi tiết: a) Hình phẳng (H) trong đề bài là hai hình tam giác vuông, với các cạnh là: - Đáy của tam giác thứ nhất: \(6 - 3 = 3\) - Chiều cao của tam giác thứ nhất: \(3 - 0 = 3\) - Đáy của tam giác thứ hai: \(3 - 1 = 2\) - Chiều cao của tam giác thứ nhất: \(0 - ( - 2) = 2\) Diện tích tam giác được tính theo công thức: \(S = \frac{1}{2} \times 3 \times 3 + \frac{1}{2} \times 2 \times 2 = \frac{9}{2} + 2 = 6,5\) b) Tính tích phân thứ nhất: \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = \left[ {\frac{{{{(x - 3)}^2}}}{2}} \right]_1^6 = \frac{9}{2} - 2 = \frac{7}{2} = 2,5\) Tính tích phân thứ hai: \(\int_1^6 | x - 3|{\mkern 1mu} dx = \int_1^3 {(3 - x)} {\mkern 1mu} dx + \int_3^6 {(x - 3)} {\mkern 1mu} dx = 2 + \frac{9}{2} = 6,5\) Nhận xét: - Tích phân thứ nhất \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = 3.5\) không phản ánh diện tích thực của hình phẳng, vì hàm số nhận giá trị âm trong khoảng từ 1 đến 3. - Tích phân thứ hai \(\int_1^6 | x - 3|{\mkern 1mu} dx = 6.5\) chính là diện tích hình phẳng tính được ở câu a, vì nó tính giá trị tuyệt đối của hàm số, tức là cả phần âm và phần dương. LT1 Trả lời câu hỏi Luyện tập 1 trang 23 SGK Toán 12 Cùng khám phá Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và các đường thẳng \(x = - 3,x = 2\). Phương pháp giải: - Xác định ình phẳng cần tính diện tích. - Phân tích dấu của hàm \(y = {x^3}\). - Tìm biểu thức diện tích tổng quát. - Tính các tích phân dựa trên biểu thức diện tích tổng quát. Lời giải chi tiết: Hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành \(y = 0\), và hai đường thẳng \(x = - 3\) và \(x = 2\). Tại các khoảng khác nhau, đồ thị có thể nằm bên trên hoặc bên dưới trục hoành, nên cần tính tích phân của giá trị tuyệt đối \(|{x^3}|\) để đảm bảo kết quả diện tích là dương. - Từ \(x = - 3\) đến \(x = 0\), \(y = {x^3}\) là âm. - Từ \(x = 0\) đến \(x = 2\), \(y = {x^3}\) là dương. Diện tích hình phẳng được tính bằng cách lấy tích phân của \(|{x^3}|\) từ \(x = - 3\) đến \(x = 2\) \(S = \int_{ - 3}^0 - {x^3}{\mkern 1mu} dx + \int_0^2 {{x^3}} {\mkern 1mu} dx\) Trong khoảng \(x \in [ - 3,0]\), đổi dấu hàm số \({x^3}\) để đảm bảo diện tích là dương. Tích phân của \( - {x^3}\) trong khoảng \([ - 3,0]\): \(\int_{ - 3}^0 - {x^3}{\mkern 1mu} dx = - \left[ {\frac{{{x^4}}}{4}} \right]_{ - 3}^0 = - \left( {\frac{{{0^4}}}{4} - \frac{{{{( - 3)}^4}}}{4}} \right) = - \left( {0 - \frac{{81}}{4}} \right) = \frac{{81}}{4}\) Tích phân của \({x^3}\) trong khoảng \(\left[ {0,{\rm{ }}2} \right]\): \(\int_0^2 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_0^2 = \frac{{{2^4}}}{4} - \frac{{{0^4}}}{4} = \frac{{16}}{4} = 4\) Diện tích tổng cộng là tổng của hai kết quả tích phân: \(S = \frac{{81}}{4} + 4 = \frac{{81}}{4} + \frac{{16}}{4} = \frac{{97}}{4}\) Vậy, diện tích của hình phẳng là: \(S = \frac{{97}}{4} = 24.25\). VD1 Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Cùng khám phá Một cái cổng có kích thước như Hình 4.14a. Vòm cổng có hình dạng một parabol có đỉnh \(I(0;2)\) và đi qua điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) như Hình 4.14b. Tính diện tích hai cánh cửa cổng.
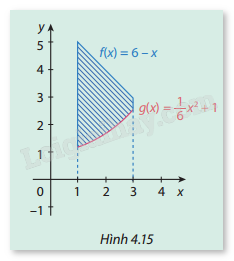
Phương pháp giải: - Xác định phương trình parabol. - Tính diện tích một cánh cửa cổng bằng cách tính tích phân diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\). - Nhân diện tích một cánh cửa với 2 để ra diện tích hai cánh cửa cổng. Lời giải chi tiết: Xác định phương trình parabol đỉnh \(I(0;2)\) có dạng: \(y = a{x^2} + 2\) Sử dụng điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) để tìm hệ số \(a\): \(\frac{3}{2} = a{\left( {\frac{5}{2}} \right)^2} + 2\) Giải ra ta được: \(a = - \frac{2}{{25}}\) Vậy phương trình của parabol là: \(y = - \frac{2}{{25}}{x^2} + 2\) Diện tích một cánh cửa là diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\), được tính bằng tích phân: \(S = 2\int_0^{\frac{5}{2}} {\left( { - \frac{2}{{25}}{x^2} + 2} \right)} dx\) Tính tích phân: \(S = 2\left[ {\left( { - \frac{2}{{25}} \cdot \frac{{{x^3}}}{3} + 2x} \right)} \right]_0^{\frac{5}{2}}\) \(S = 2\left[ { - \frac{2}{{25}} \cdot \frac{{125}}{{24}} + 2 \cdot \frac{5}{2}} \right]\) \(S = 2\left( { - \frac{5}{{12}} + 5} \right) = 2\left( {\frac{{55}}{{12}}} \right) = \frac{{55}}{6}\) Vậy, diện tích hai cánh cửa cổng là: \(9,167{{\rm{m}}^2}\). HĐ2 Trả lời câu hỏi Hoạt động 2 trang 24 SGK Toán 12 Cùng khám phá Cho hai hàm số \(f(x) = 6 - x\), \(g(x) = \frac{1}{6}{x^2} + 1\). a) Tính \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = f\left( x \right).\) b) Tính \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = g\left( x \right).\) c) Qua \({S_1},\,\,{S_2}\) tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right),{\rm{ }}y = g\left( x \right)\) và các đường thẳng \(x = 1,{\rm{ }}x = 3\). (phần hình phẳng được gạch chéo trong Hình 4.15).
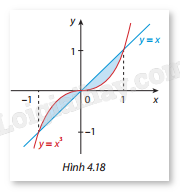
Phương pháp giải: a) Tính diện tích \({S_1}\) bằng cách lấy tích phân của hàm số \(f(x) = 6 - x\) từ \(x = 1\) đến \(x = 3\) b) Tính diện tích \({S_2}\) bằng cách lấy tích phân của hàm số \(g(x) = \frac{1}{6}{x^2} + 1\) từ \(x = 1\) đến \(x = 3\). c) Tính diện tích hình phẳng giới hạn bởi hai đồ thị bằng cách lấy hiệu diện tích \({S_1} - {S_2}\). Lời giải chi tiết: a) Tính \({S_1}\) Diện tích \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = f(x)\): \({S_1} = \int_1^3 {(6 - x)} dx\) Tính tích phân: \({S_1} = \left[ {6x - \frac{{{x^2}}}{2}} \right]_1^3\) \({S_1} = \left( {6 \cdot 3 - \frac{{{3^2}}}{2}} \right) - \left( {6 \cdot 1 - \frac{{{1^2}}}{2}} \right)\) \({S_1} = (18 - 4.5) - (6 - 0.5) = 13.5 - 5.5 = 8\) b) Tính \({S_2}\) Diện tích \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = g(x)\): \({S_2} = \int_1^3 {\left( {\frac{1}{6}{x^2} + 1} \right)} dx\) Tính tích phân: \({S_2} = \left[ {\frac{1}{6} \cdot \frac{{{x^3}}}{3} + x} \right]_1^3\) \({S_2} = \left( {\frac{1}{6} \cdot \frac{{27}}{3} + 3} \right) - \left( {\frac{1}{6} \cdot \frac{1}{3} + 1} \right)\) \({S_2} = \left( {\frac{9}{6} + 3} \right) - \left( {\frac{1}{{18}} + 1} \right)\) \({S_2} = (1.5 + 3) - \left( {\frac{1}{{18}} + 1} \right) = 4.5 - \frac{{19}}{{18}} = \frac{{81}}{{18}} - \frac{{19}}{{18}} = \frac{{62}}{{18}} \approx 3,44\) c) Tính diện tích hình phẳng giữa hai đồ thị Diện tích hình phẳng giới hạn bởi hai đồ thị \(f(x)\) và \(g(x)\) trong khoảng \(x = 1\) đến \(x = 3\) là: \(S = {S_1} - {S_2} = 8 - 3,44 = 4,56\) Vậy, diện tích hình phẳng giữa hai đồ thị là \(S = 4,56\). LT2 Trả lời câu hỏi Luyện tập 2 trang 26 SGK Toán 12 Cùng khám phá Tính diện tích hình phẳng được tô màu trong Hình 4.18.
Phương pháp giải: - Xác định giao điểm của hai đường \(y = {x^3}\) và \(y = x\) bằng cách giải phương trình: \({x^3} = x\) - Diện tích hình phẳng giữa hai đường cong \(y = {x^3}\) và \(y = x\) trong khoảng từ \(x = - 1\) đến \(x = 1\) được tính bằng: \(S = \int_{ - 1}^1 | x - {x^3}|{\mkern 1mu} dx\) Lời giải chi tiết: Giao điểm của hai đường \(y = {x^3}\) và \(y = x\) là: \({x^3} = x \Leftrightarrow x({x^2} - 1) = 0\) Suy ra: \(x = 0\), \(x = 1\), và \(x = - 1\). Vì trên khoảng từ \( - 1\) đến 0, \(y = {x^3}\) nằm trên \(y = x\), và trên khoảng từ 0 đến 1, \(y = x\) nằm trên \(y = {x^3}\), ta có: \(S = \int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx + \int_0^1 {(x - {x^3})} {\mkern 1mu} dx\) Tính tích phân: \(\int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right]_{ - 1}^0 = \left( {0 - 0} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) = - \frac{1}{4} + \frac{1}{2} = \frac{1}{4}\) \(\int_0^1 {(x - {x^3})} {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{4}} \right]_0^1 = \left( {\frac{1}{2} - \frac{1}{4}} \right) - (0 - 0) = \frac{1}{4}\) Vậy diện tích hình phẳng là: \(S = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
|




















Danh sách bình luận