Giải bài tập 4.20 trang 31 SGK Toán 12 tập 2 - Cùng khám pháCho hàm số \(y = f(x)\) có đồ thị như Hình 4.27 và diện tích hai phần \[A,{\rm{ }}B\] lần lượt bằng 11 và 2. Tính \(\int_{ - 2}^1 f (x)dx\). Quảng cáo
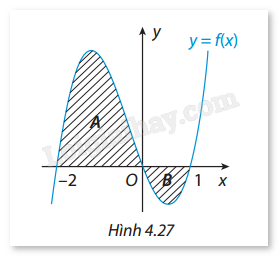
Đề bài Cho hàm số \(y = f(x)\) có đồ thị như Hình 4.27 và diện tích hai phần \(A,{\rm{ }}B\) lần lượt bằng 11 và 2. Tính \(\int_{ - 2}^1 f (x)dx\).
Phương pháp giải - Xem chi tiết - Xác định dấu của \(f(x)\) trên các khoảng \([ - 2,0]\) và \([0,1]\). - Tính tích phân từ -2 đễn 1 dựa vào diện tích đã cho. Lời giải chi tiết - Từ đồ thi, \(A\) ở bên trái trục tung \((x = 0)\) và diện tích của \(A\) là 11 (dương). - Phằn \(B\) nằm phía bên phải và diện tích của \(B\) là 2 (âm do đồ thị ở dưới trục \(x\)). - Tích phân từ -2 đến 1 của \(f(x)\): \(\int_{ - 2}^1 f (x)dx = 11 - 2 = 9\).
|




















Danh sách bình luận