Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều

Đề bài

 

Khảo sát sự biến thiên của các hàm số sau:

a, \(y = \frac{{x - 1}}{{x + 1}}\)

b,\(y = \frac{{ - 2x}}{{x + 1}}\)

c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\)

d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)

e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)

g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)

Lời giải chi tiết

a) \(y = \frac{{x - 1}}{{x + 1}}\)

1) TXĐ: \(x \in \mathbb{R}\left\{ { - 1} \right\}\)

2) Sự biến thiên

\(y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\;\) với mọi \(x \ne  - 1\)

Bảng biến thiên:

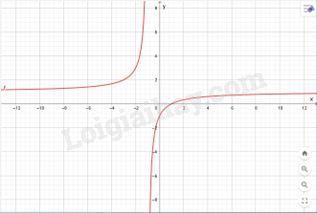
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)

Hàm số không có cực trị

3) Đồ thị

Giao điểm đồ thị với trục tung: \(\left( {0; - 1} \right)\)

Giao điểm đồ thị với trục hoành: \(\left( {1;0} \right)\)

Đồ thị đi qua các điểm: \(\left( {0; - 1} \right)\), \(\left( {1;0} \right)\)

b) \(y = \frac{{ - 2x}}{{x + 1}}\)

1) TXĐ: \(x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)

2) Sự biến thiên

 với mọi \(x \ne  - 1\)

Bảng biến thiên:

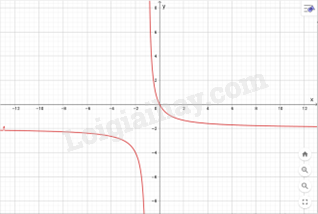
Hàm số nghịch biến trên khoảng \(\left( { - \infty , - 1} \right) \cup \left( { - 1,\infty } \right)\)

3) Đồ thị

Giao điểm đồ thị với trục tung: \(\left( {0;0} \right)\)

Giao điểm đồ thị với trục hoành: \(\left( {0;0} \right)\)

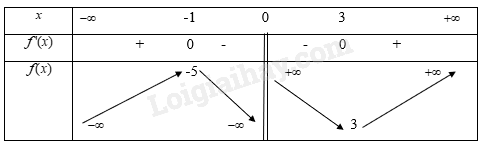
c) \(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\)

1) TXĐ: \(x \in \mathbb{R}\backslash \left\{ 1 \right\}\)

2) Sự biến thiên

Ta có \(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\)\( = x - 2 + \frac{4}{{x - 1}}\)

\(y' = 1 - \frac{4}{{{{(x - 1)}^2}}}\)\( = \frac{{{x^2} - 2x - 3}}{{{{(x - 1)}^2}}}\)

Xét \(y' = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\)

Bảng biến thiên

Hàm số đồng biến trên khoảng \(\left( { - \infty , - 1} \right),\left( {3, + \infty } \right)\). Nghịch biến trên khoảng \(\left( { - 1,1} \right),\left( {1,3} \right)\)

3) Đồ thị

Giao điểm đồ thị với trục tung: \(\left( {0; - 6} \right)\)

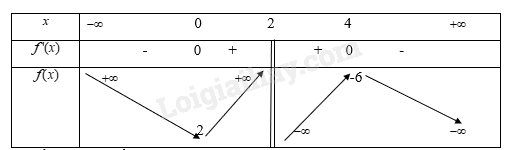
d) \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)

Hàm số trên xác định trên R\{2}

Ta có \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)\( =  - x - \frac{4}{{x - 2}}\)

          \(y' =  - 1 + \frac{4}{{{{(x - 2)}^2}}}\)\( = \frac{{ - {x^2} + 4x}}{{{{(x - 2)}^2}}}\)

Xét \(y' = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\)

Từ đó ta có bảng biến thiên là

Từ bảng biến thiên ta thấy

Hàm số đồng biến \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)trên các khoảng \((0;2)\) và \((2;4)\)

Hàm số nghịch biến \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)trên các khoảng \(( - \infty ;0)\) và \((4; + \infty )\)

Ta có đồ thị hàm số là

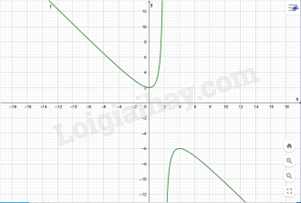
e) \(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)

Hàm số xác định trên R\{-2}

Ta có \(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\) \( = 2x - \frac{{x + 5}}{{x + 2}}\)

           \(y' = 2 + \frac{3}{{{{(x + 2)}^2}}}\)

Vì \(y' > 0\)với \(x \in R/\left\{ { - 2} \right\}\)

Nên hàm số luôn đồng biến với \(x \in R/\left\{ { - 2} \right\}\)

Ta có đồ thị hàm số là

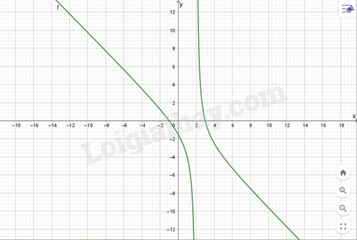
g) \(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)

Hàm số xác định trên R/{2}

Ta có : \(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\) \( =  - x + \frac{3}{{x - 2}}\)

           \(y' =  - 1 - \frac{3}{{{{(x - 2)}^2}}}\)

Vì \(y' < 0\)với \(x \in R/\left\{ 2 \right\}\)

Nên hàm số luôn nghịch biến với \(x \in R/\left\{ 2 \right\}\)

Ta có đồ thị hàm số là