Giải bài tập 5 trang 42 SGK Toán 12 tập 1 - Cánh diềukhảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau: (a,;y = 2{x^3} - 3x + 1 b,;y = - {x^3} + 3x - 1) c, ( y = {left( {x - 2} right)^3} + 4) d,(y = - {x^3} + 3{x^2} - 1) e, (y = frac{1}{3}{x^3} + {x^2} + 2x + 1) g,( y = - {x^3} - 3x) Quảng cáo
Đề bài
Khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = 2{x^3} - 3{x^2} + 1\); b) \(y = - {x^3} + 3{x^2} - 1\); c) \( y = {\left( {x - 2} \right)^3} + 4\); d) \(y = - {x^3} + 3{x^2} - 3x + 2\); e) \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1\); g) \( y = - {x^3} - 3x\). Phương pháp giải - Xem chi tiết Tìm TXĐ. Xét sự biến thiên. Vẽ đồ thị. Lời giải chi tiết a) \(y = 2{x^3} - 3{x^2} + 1\). Tập xác định: D = R. \(y' = 6{x^2} - 6x\); \(y' = 0 \Rightarrow \left[ \begin{array}{l}x = 1 \\x = 0\end{array} \right.\) Bảng biến thiên:
Đồ thị hàm số:
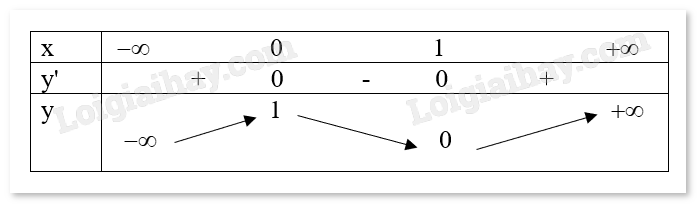
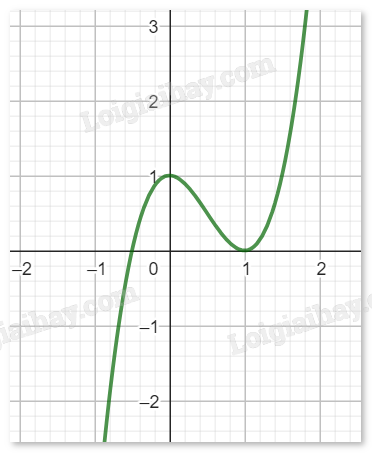
b) \(y = - {x^3} + 3{x^2} - 1\). Tập xác định: D = R. \(y' = - 3{x^2} + 6x\); \(y' = 0 \Rightarrow \left[ {\begin{array}xx = 0\\x = 2\end{array}} \right.\) Bảng biến thiên:
Đồ thị hàm số:
c) \(y = {\left( {x - 2} \right)^3} + 4\). Tập xác định: D = R. \(y' = 3{\left( {x - 2} \right)^2} \), \(y’=0 \Rightarrow {\left( {x\;-\;2} \right)^2} = 0 \Rightarrow x = 2\). Bảng biến thiên:
Đồ thị hàm số:
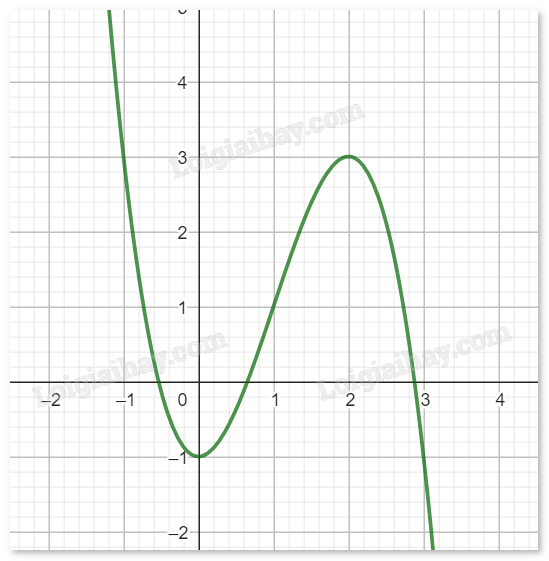
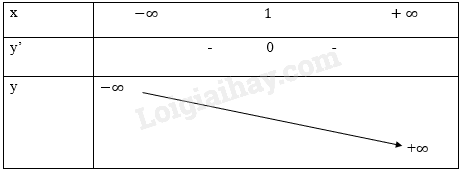
d) \(y = - {x^3} + 3{x^2} - 3x + 2\). Tập xác định: D = R. \(y' = - 3{x^2} + 6x - 3\); \(y' = 0 \Rightarrow x = 1\). Bảng biến thiên:
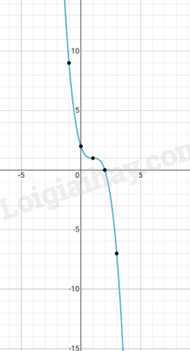
Đồ thị hàm số:
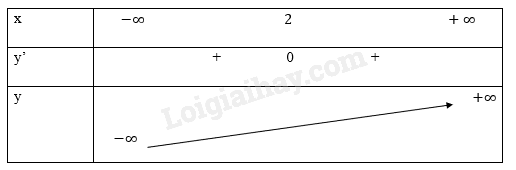
e) \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1 \Rightarrow y' = {x^2} + 2x + 2 > 0, \forall x \in D\). Tập xác định: D = R.
Đồ thị hàm số:
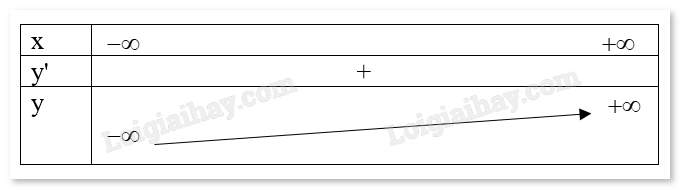
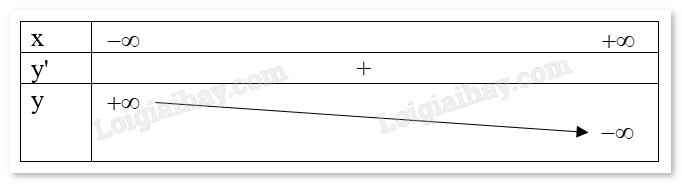
g) \(y = - {x^3} - 3x \Rightarrow y' = - 3{x^2} - 3 < 0, \forall x \in D\). Tập xác định: D = R. Bảng biến thiên:
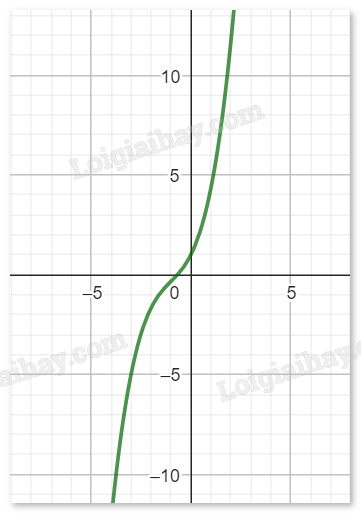
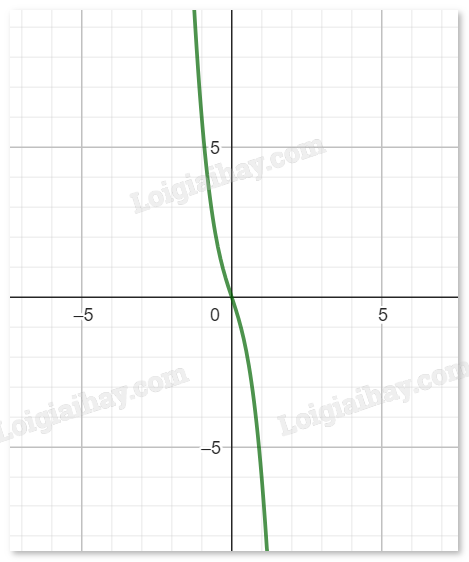
Đồ thị hàm số:
|






















Danh sách bình luận