Giải bài tập 5 trang 8 SGK Toán 12 tập 2 - Cánh diềuTại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số (B'(t) = 20{t^3} - 300{t^2} + 1000t) trong đó t tính bằng giờ ((0 le t le 15)), B’(t) tính bằng khách/giờ Sau một giờ, 500 người đã có mặt tại lễ hội a) Viết công thức của hàm số B(t) biểu diễn số lượng khách tham dự lễ hội với (0 le t le 15) b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội? c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu? d) Tại thời điểm nào thì tốc độ thay đổi lượn Quảng cáo
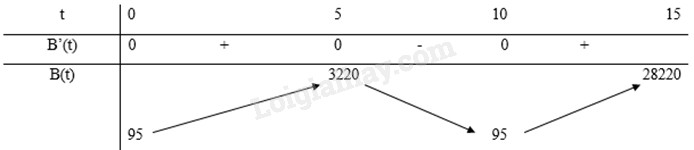
Đề bài Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số \(B'(t) = 20{t^3} - 300{t^2} + 1000t\), trong đó t tính bằng giờ (\(0 \le t \le 15\)), B’(t) tính bằng khách/giờ. Biết rằng sau một giờ, 500 người đã có mặt tại lễ hội. a) Viết công thức của hàm số B(t) biểu diễn số lượng khách tham dự lễ hội với \(0 \le t \le 15\). b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội? c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu? d) Tại thời điểm nào thì tốc độ thay đổi lượng khách tham gia dự lễ hội là lớn nhất? Phương pháp giải - Xem chi tiết a) Áp dụng công thức tìm nguyên hàm của một hàm số. b) Thay số vào công thức đã tìm được ở phần a). c) Khảo sát hàm số B(t) để tìm GTLN. d) Khảo sát hàm số B’(t) để tìm GTLN. Lời giải chi tiết a) \(\int {B'(t)} dt = \int {\left( {20{t^3} - 300{t^2} + 1000t} \right)} dt \) \(= 5{t^4} - 100{t^3} + 500{t^2} + C\). \(B(1) = 500 \Leftrightarrow 5 - 100 + 500 + C = 500 \Leftrightarrow C = 95\). Vậy \(B(t) = 5{t^4} - 100{t^3} + 500{t^2} + 95\). b) \(B(3) = {5.3^4} - {100.3^3} + {500.3^2} + 95 = 2300\). Vậy sau 3h sẽ có 2300 khách tham dự lễ hội. c) Số lượng khách tham dự lễ hội lớn nhất chính là giá trị lớn nhất của hàm số B(t) trên đoạn [0; 15]. \(B'(t) = 20{t^3} - 300{t^2} + 1000t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 5\\t = 10\end{array} \right.\) Bảng biến thiên:
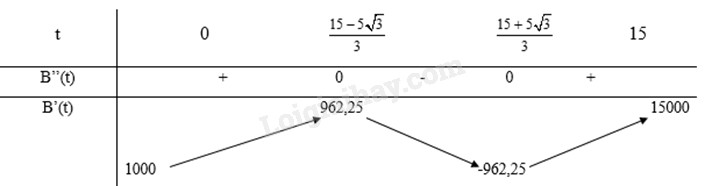
Từ bảng biển thiên ta thấy, B(t) max tại t = 15. Vậy số lượng khách tham dự lớn nhất là: 28220 khách. d) \(B''(t) = 60{t^2} - 600t + 1000 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \frac{{15 - 5\sqrt 3 }}{3}\\t = \frac{{15 + 5\sqrt 3 }}{3}\end{array} \right.\) Bảng biến thiên:
Từ bảng biển thiên ta thấy, B’(t) max tại t = 15. Vậy tại thời điểm t = 15 giờ thì tốc độ thay đổi lượng khách tham gia dự lễ hội là lớn nhất.
|




















Danh sách bình luận