Giải bài 9.7 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2

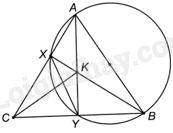
Đề bài

Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B).

a) Chứng minh rằng tam giác CXY cân tại Y.

b) Cho BX cắt AY tại K. Chứng minh rằng CK vuông góc với AB.

Lời giải chi tiết

a) Vì góc AXB và góc AYB là các góc nội tiếp cùng chắn nửa đường tròn đường kính AB nên \(\widehat {AXB} = \widehat {AYB} = {90^o}\). Do đó, \(AY \bot BC,BX \bot AC\).

Vì tam giác ABC cân tại A nên AY là đường cao đồng thời là đường trung tuyến của tam giác.

Do đó, Y là trung điểm của BC.

Suy ra, Y là tâm đường tròn ngoại tiếp tam giác vuông BXC vuông tại X. Do đó, \(YC = YX\).

Suy ra, tam giác CXY cân tại Y.

b) Vì AY, BX là các đường cao của tam giác ABC cắt nhau tại K nên K là trực tâm của tam giác ABC. Do đó, CK vuông góc với AB.