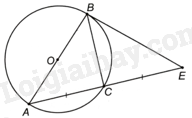
Giải bài 9.6 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2

Đề bài

Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng \(BE = BA\).

Lời giải chi tiết

Vì ACB là góc nội tiếp chắn nửa đường tròn (O) nên \(\widehat {ACB} = {90^o}\), suy ra \(BC \bot AE\) nên \(\widehat {BCE} = {90^o}\).

Vì E đối xứng của A qua C nên \(CA = CE\).

Tam giác BCA và tam giác BCE có: \(\widehat {BCA} = \widehat {BCE} = {90^o}\), \(CA = CE\), BC chung.

Suy ra \(\Delta BCA = \Delta BCE\left( {c.g.c} \right)\). Do đó, \(BE = BA\).