Giải bài 9.32 trang 109 SGK Toán 8 tập 2 - Kết nối tri thức

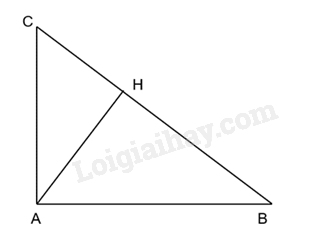
Đề bài

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH=16cm, CH=9cm

a) Tính độ dài đoạn thẳng AH

b) Tính độ dài đoạn thằng AB và AC

Lời giải chi tiết

a) Có BC=BH+CH=16+9=25

Xét tam giác AHC vuông tại H có: $A{H^2} = A{C^2} - C{H^2}$(định lý Pythagore) (1)

Xét tam giác AHB vuông tại H có: $A{H^2} = A{B^2} - B{H^2}$ (định lý Pythagore) (2)

Xét (1) + (2), có:

$\begin{array}{l}2{\rm{A}}{H^2} = A{C^2} - C{H^2} + A{B^2} - B{H^2}\\2{\rm{A}}{H^2} = B{C^2} - C{H^2} - B{H^2}\\2{\rm{A}}{H^2} = {25^2} - {9^2} - {16^2}\\2{\rm{A}}{H^2} = 288\end{array}$

AH=12(cm)

b) Có $A{C^2} = A{H^2} + C{H^2}$ (định lý Pythagore) 

=> $A{C^2} = {12^2} + {9^2} = 225$

=> AC=15(cm)

Có  $A{B^2} = A{H^2} + B{H^2}$ (định lý Pythagore) 

=> $A{B^2} = {12^2} + {16^2} = 400$

=> AB=20(cm)