Bài 9 trang 73 Vở bài tập toán 8 tập 2

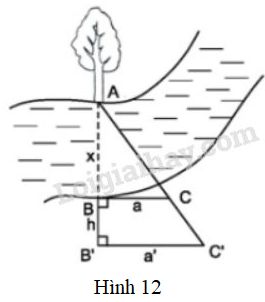
Đề bài

Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?

Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h12). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách \(AB = x\) theo \(BC = a, B'C'= a', BB'= h\).

Lời giải chi tiết

Mô tả cách làm:

* Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và \(AB\) chính là khoảng cách cần đo.

* Trên hai đường thẳng vuông góc với \(AB'\) tại \(B\) và \(B'\) lấy \(C\) và \(C'\) sao cho \(A,C,C'\) thẳng hàng.

* Đo độ dài các đoạn \(BB'= h, BC= a, B'C'= a'\). Từ đó ta sẽ tính được đoạn \(AB=x.\)

Giải thích: 

Ta có: \(BC ⊥ AB’\) và \(B’C’ ⊥ AB’ ⇒ BC // B’C’\)

Xét \(ΔAB’C’\) có \(BC // B’C’ \,(B ∈ AB’, C ∈ AC’) \) 

\(⇒ \dfrac{AB}{AB'} = \dfrac{BC}{BC'}\) (hệ quả định lý Talet) mà \(AB' = x + h\) nên 

\(\dfrac{x}{x+ h} = \dfrac{a}{a'}\) 

\( \Leftrightarrow  a'x = ax + ah\)

\( \Leftrightarrow  a'x - ax = ah\)

\(\Leftrightarrow  x(a' - a) = ah\)

\( \Rightarrow x= \dfrac{ah}{a'-a}\)

Vậy khoảng cách \(AB\) bằng \(\dfrac{ah}{a'-a}\)

Loigiaihay.con