Giải bài 9 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2Trong hình bên, cho AC=8cm, AD=9,6cm, (widehat {ABC} = {90^o},widehat {ACB} = {54^o}) và (widehat {ACD} = {74^o}). Hãy tính: a) AB (làm tròn đến hàng phần nghìn của cm). b) (widehat {ADC}) (làm tròn đến phút). (Gợi ý: Kẻ đường cao AH của tam giác ACD). Quảng cáo
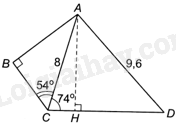
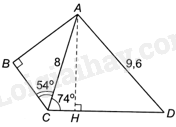
Đề bài Trong hình bên, cho AC=8cm, AD=9,6cm, \(\widehat {ABC} = {90^o},\widehat {ACB} = {54^o}\) và \(\widehat {ACD} = {74^o}\). Hãy tính: a) AB (làm tròn đến hàng phần nghìn của cm). b) \(\widehat {ADC}\) (làm tròn đến phút). (Gợi ý: Kẻ đường cao AH của tam giác ACD).
Phương pháp giải - Xem chi tiết a) Trong tam giác ABC vuông tại B, ta có: \(AB = AC.\sin ACB\). b) + Kẻ đường cao AH của tam giác ACD, ta có: \(AH = AC\sin ACD\) nên tính được AH. + Ta có: \(\sin D = \frac{{AH}}{{AD}}\), từ đó tính được góc ADC. Lời giải chi tiết
a) Trong tam giác ABC vuông tại B, ta có: \(AB = AC.\sin ACB = 8.\sin {54^o} \approx 6,472\left( {cm} \right)\). b) Kẻ đường cao AH của tam giác ACD, ta có: \(AH = AC\sin ACD = 8.\sin {74^o} \approx 7,690\left( {cm} \right)\). Ta có: \(\sin D = \frac{{AH}}{{AD}} \approx \frac{{7,69}}{{9,6}} \approx 0,801\) nên \(\widehat {ADC} = {53^o}14'\).
|




















Danh sách bình luận