Giải bài 14 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2Cho tam giác ABC nội tiếp đường tròn (O), vẽ (AX bot BC) và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho (DH = DX). Cho BH cắt AC tại E và CH cắt AB tại F. a) Chứng minh rằng H là trực tâm của tam giác ABC. b) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF. Quảng cáo
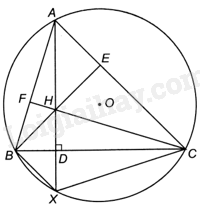
Đề bài Cho tam giác ABC nội tiếp đường tròn (O), vẽ \(AX \bot BC\) và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho \(DH = DX\). Cho BH cắt AC tại E và CH cắt AB tại F. a) Chứng minh rằng H là trực tâm của tam giác ABC. b) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF. Phương pháp giải - Xem chi tiết a) + Chứng minh \(\Delta BDH = \Delta BDX\left( {c.g.c} \right)\)nên \(\widehat {HBD} = \widehat {DBX}\). + Mà \(\widehat {CBX} = \widehat {CAX}\) nên \(\widehat {HBD} = \widehat {CAX} = {90^o} - \widehat {ACB}\). + Chứng minh \(\widehat {BEC} = {90^o}\). Do đó, \(BE \bot AC\). + Chứng minh tương tự ta có: \(CF \bot AB\). + Do đó, H là trực tâm của tam giác ABC. b) + Chứng minh tứ giác HDBF nội tiếp đường tròn đường kính BH, suy ra \(\widehat {HDF} = \widehat {HBF}\). + Tương tự ta có: \(\widehat {HDE} = \widehat {HCE}\). Mà \(\widehat {HBF} = {90^o} - \widehat {BAC} = \widehat {HCE}\) nên \(\widehat {HDF} = \widehat {HBF} = \widehat {HCE} = \widehat {HDE}\), suy ra H nằm trên đường phân giác của góc EDF của tam giác DEF. + Tương tự ta có: H nằm trên các đường phân giác của các góc DEF, DFE. Do đó, H là tâm đường tròn nội tiếp tam giác DEF. Lời giải chi tiết
a) Tam giác BDH và tam giác BDX có: BD là cạnh chung, \(\widehat {BDH} = \widehat {BDX} = {90^o},DH = DX\) nên \(\Delta BDH = \Delta BDX\left( {c.g.c} \right)\), suy ra \(\widehat {HBD} = \widehat {DBX}\). Mặt khác \(\widehat {CBX} = \widehat {CAX}\) (hai góc nội tiếp (O) cùng chắn cung CX). Do đó, \(\widehat {HBD} = \widehat {CAX} = {90^o} - \widehat {ACB}\). Tam giác BEC có: \(\widehat {BEC} = {180^o} - \widehat {EBC} - \widehat {ACB} = {180^o} - {90^o} + \widehat {ACB} - \widehat {ACB} = {90^o}\). Do đó, \(BE \bot AC\). Chứng minh tương tự ta có: \(CF \bot AB\). Do đó, H là trực tâm của tam giác ABC. b) Do \(\widehat {HDB} = \widehat {HFB} = {90^o}\) nên tứ giác HDBF nội tiếp đường tròn đường kính BH. Do đó, \(\widehat {HDF} = \widehat {HBF}\) (hai góc nội tiếp cùng chắn cung HF của đường tròn đường kính BH). Tương tự ta có: \(\widehat {HDE} = \widehat {HCE}\). Mặt khác, \(\widehat {HBF} = {90^o} - \widehat {BAC} = \widehat {HCE}\). Do đó, \(\widehat {HDF} = \widehat {HBF} = \widehat {HCE} = \widehat {HDE}\). Vậy H nằm trên đường phân giác của góc EDF của tam giác DEF. Tương tự, H nằm trên các đường phân giác của các góc DEF, DFE. Do đó, H là tâm đường tròn nội tiếp tam giác DEF.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
