Giải bài 18 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2Một đoàn tàu có 4 toa A, B, C, D đỗ ở một sân ga. Trên sân ga có hai hành khách không quen biết nhau. Từ sân ga, mỗi người chọn ngẫu nhiên một toa tàu để bước lên. Kí hiệu hai hành khách là 1 và 2. Mỗi kết quả có thể là một cặp (X, Y), trong đó X, Y tương ứng là toa tàu mà hành khách số 1 và hành khác số 2 bước lên. a) Có bao nhiêu kết quả có thể xảy ra? Chúng có đồng khả năng không? Tại sao? b) Mô tả không gian mẫu. c) Tính xác suất của các biến cố sau: + E: “Hai hành khách này ở cùng một t Quảng cáo
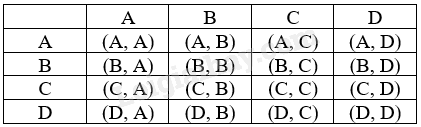
Đề bài Một đoàn tàu có 4 toa A, B, C, D đỗ ở một sân ga. Trên sân ga có hai hành khách không quen biết nhau. Từ sân ga, mỗi người chọn ngẫu nhiên một toa tàu để bước lên. Kí hiệu hai hành khách là 1 và 2. Mỗi kết quả có thể là một cặp (X, Y), trong đó X, Y tương ứng là toa tàu mà hành khách số 1 và hành khác số 2 bước lên. a) Có bao nhiêu kết quả có thể xảy ra? Chúng có đồng khả năng không? Tại sao? b) Mô tả không gian mẫu. c) Tính xác suất của các biến cố sau: + E: “Hai hành khách này ở cùng một toa tàu”; + F: “Cả hai hành khách đều không lên toa tàu B”. Phương pháp giải - Xem chi tiết a, b) + Sử dụng kiến thức về không gian mẫu của phép thử để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử gọi là không gian mẫu của phép thử + Sử dụng lập bảng để tìm không gian mẫu. c) Cách tính xác suất của một biến cố E: Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \). Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng. Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E. Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \). Lời giải chi tiết a) Ta có bảng sau:
Mỗi ô trong bảng thể hiện một kết quả có thể. Chẳng hạn ô (C, B) nghĩa là hành khách số 1 chọn toa C, hành khách số 2 chọn toa B. Các kết quả có thể là đồng khả năng do mỗi hành khách chọn ngẫu nhiên một toa tàu để bước lên. b) Không gian mẫu \(\Omega \) là tập hợp 16 ô trên: \(\Omega =\{(A, A), (A, B), (A, C), (A, D), \\(B, A), (B, B), (B, C), (B, D), \\(C, A), (C, B), (C, C), (C, D), \\(D, A), (D, B), (D, C), (D, D)\}.\) c) + Có 4 kết quả thuận lợi cho biến cố E là: (A, A), (B, B), (C, C), (D, D) nên \(P\left( E \right) = \frac{4}{{16}} = \frac{1}{4}\). + Có 9 kết quả thuận lợi cho biến cố F là: (A, A), (A, C), (A, D), (C, A), (C, C), (C, D), (D, A), (D, C), (D, D) nên \(P\left( F \right) = \frac{9}{{16}}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
