Giải bài 13 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2Đề bài Cho tam giác nhọn ABC nội tiếp đường tròn (O). Ba đường cao AD, BE và CF của tam giác ABC cắt nhau tại H. Gọi AK là đường kính của (O). Chứng minh rằng: a) (BH = CK,CH = BK); b) (AD.AK = AB.AC). Quảng cáo
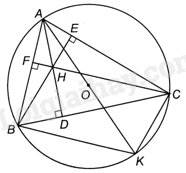
Đề bài Cho tam giác nhọn ABC nội tiếp đường tròn (O). Ba đường cao AD, BE và CF của tam giác ABC cắt nhau tại H. Gọi AK là đường kính của (O). Chứng minh rằng: a) \(BH = CK,CH = BK\); b) \(AD.AK = AB.AC\). Phương pháp giải - Xem chi tiết a) Chứng minh BH//KC, CH//KB, suy ra BHCK là hình bình hành. Do đó, \(BH = CK,CH = BK\). b) Chứng minh $\Delta ABD\backsim \Delta AKC\left( g.g \right)$, từ đó suy ra \(AD.AK = AB.AC\). Lời giải chi tiết
a) Xét (O): \(\widehat {ACK} = \widehat {ABK} = {90^o}\) (góc nội tiếp chắn nửa đường tròn). Suy ra: \(AC \bot CK, AB \bot KB\). Mặt khác, \(AC \bot BH,\)\(AB \bot CH\). Do đó, BH//KC, CH//KB. Suy ra, BHCK là hình bình hành. Do đó, \(BH = CK, CH = BK\). b) Hai tam giác ABD và AKC có: \(\widehat {ADB} = \widehat {ACK} = {90^o},\widehat {ABD} = \widehat {AKC}\) (góc nội tiếp của (O) cùng chắn cung AC). Suy ra, $\Delta ABD\backsim \Delta AKC\left( g.g \right)$, suy ra \(\frac{{AB}}{{AK}} = \frac{{AD}}{{AC}}\), do đó \(AD.AK = AB.AC\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
