Trang chủ
SBT Toán 9 - giải SBT Toán 9 - Cánh diều

Giải bài 8 trang 125 sách bài tập toán 9 - Cánh diều tập 2

Bác An cần đúc một ống cống thoát nước bằng bê tông có dạng hình trụ rỗng với đường kính đường tròn đáy ngoài là 0,8 m, chiều dài ống là 1,5 m và bề dày là 0,1 m (Hình 7). Hỏi số tiền bác An cần dùng để làm được một ống cống như thế là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)? Biết giá loại bê tông bác An sử dụng là 1 000 000 đồng một mét khối.

Quảng cáo

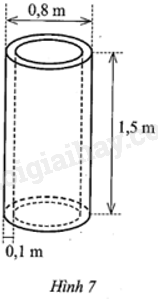
Đề bài

Bác An cần đúc một ống cống thoát nước bằng bê tông có dạng hình trụ rỗng với đường kính đường tròn đáy ngoài là 0,8 m, chiều dài ống là 1,5 m và bề dày là 0,1 m (Hình 7).

Hỏi số tiền bác An cần dùng để làm được một ống cống như thế là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)? Biết giá loại bê tông bác An sử dụng là 1 000 000 đồng một mét khối.

Phương pháp giải - Xem chi tiết

Dựa vào: Thể tích hình trụ: \(V = \pi {r^2}h\).

Lời giải chi tiết

Bán kính đáy của hình trụ bên ngoài là: 0,8 : 2 = 0,4 (m).

Hình trụ (bên ngoài) với bán kính đáy 0,4 m, chiều cao 1,5 m có thể tích là:

πr2h = π . (0,4)2 . 1,5 = 0,24π (m3).

Do bề dày của ống cống là 0,1 m nên đường kính đường tròn đáy của hình trụ (bên trong) là: 0,8 – 0,1 – 0,1 = 0,6 (m).

Bán kính đáy của hình trụ bên trong là: 0,6 : 2 = 0,3 (m).

Hình trụ (bên trong) với bán kính đáy 0,3 m, chiều cao 1,5 m có thể tích là:

πr2h = π . (0,3)2 . 1,5 = 0,135π (m3).

Lượng bê tông cần dùng để đúc ống cống đó là:

0,24π – 0,135π = 0,105π (m3).

Số tiền bác An cần dùng để làm được một ống cống như yêu cầu là:

0,105π . 1 000 000 = 105 000π ≈ 105 000.3,14 = 329 700 ≈ 330 000 (đồng).

  • Giải bài 9 trang 126 sách bài tập toán 9 - Cánh diều tập 2

    Để đo thể tích một tượng đồng, người ta đã thả chìm tượng đồng vào thùng nước hình trụ có bán kính đường tròn đáy là 6 dm. Hỏi thể tích tượng đồng là bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)? Biết khi thả chìm tượng đồng vào thùng nước thì lượng nước trong thùng dâng cao 5 dm và nước vẫn không bị trào ra khỏi miệng thùng.

  • Giải bài 10 trang 126 sách bài tập toán 9 - Cánh diều tập 2

    Bác An có một bình hình trụ to với chiều cao h (cm). Bác đặt một bình cây thuỷ sinh cũng có dạng hình trụ với chiều cao h (cm) vào bên trong bình hình trụ to đó. Bình cây thuỷ sinh có bán kính đáy bằng một nửa bán kính đáy bình hình trụ to. Bác An dùng phần không gian giữa hai bình hình trụ đó để nuôi cá cảnh (Hình 8). Tính tỉ số thể tích phần không gian nuôi cá cảnh và thể tích bình hình trụ to (coi bề dày đáy của các bình hình trụ không đáng kể).

  • Giải bài 11 trang 126 sách bài tập toán 9 - Cánh diều tập 2

    Các kích thước của hai hình trụ (T) và (T’) (hình trụ (T) ở bên ngoài và hình trụ (T’) ở bên trong) được cho ở Hình 9. a) Viết biểu thức tính thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h. b) Tính chiều cao h, biết a = 16 cm, (b = frac{3}{4}a) và thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3.

  • Giải bài 12 trang 126 sách bài tập toán 9 - Cánh diều tập 2

    Tìm các hình ảnh hình trụ trong thực tế.

  • Giải bài 7 trang 125 sách bài tập toán 9 - Cánh diều tập 2

    Một hình trụ (T) có thể tích 81π cm3 và có đường sinh gấp ba lần bán kính đường tròn đáy. Tính độ dài đường sinh của (T).

Quảng cáo
Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
close